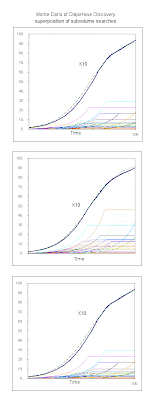
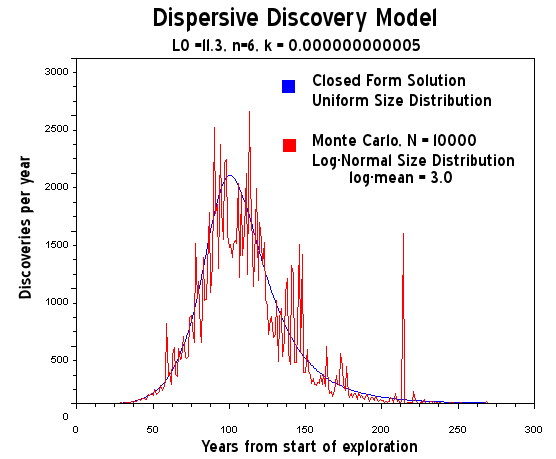
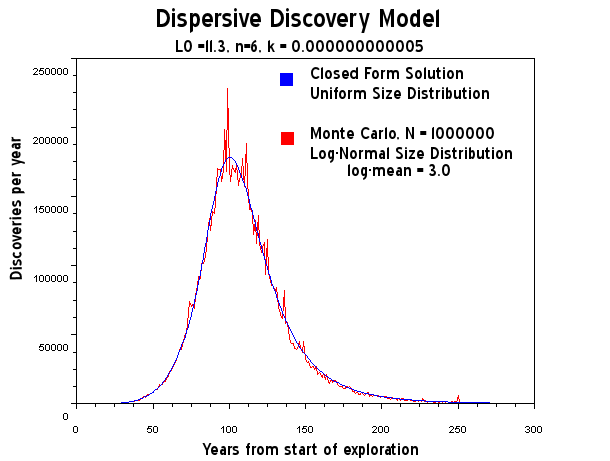
Alternate title:
Solving the slippery nature of the bathtub curve.To reset the stage, I think I have a fairly solid model for oil discovery. The basic premise involves adding a level of uncertainty to search rates and then accelerating the mean through a volume of search space. This becomes the
Dispersive Discovery model.
As I started looking at dispersion to explain the process of oil discovery, it seemed likely that it would eventually lead to the field of reliability. You see, for every success you have a failure. We don't actively seek a failure, but they lie ready to spring forth at some random unforeseen time. In other words, we can never predict when a failure occurs; just as when we look for something at random -- like an oil reservoir, we will never absolutely know when we will find it.
So the same dispersion in search rates leading to a successful oil find also leads to the occurrence -- in that same parallel upside-down universe -- of a failure. As we saw in the last post, what is the seemingly random
popping of a popcorn kernel but a failure to maintain its hard shell robustness? And by the same line of reasoning, what is a random discovery but a failure by nature to conceal its inner secrets from an intrepid prospector?
The Classic Failure Premise: The classic approximation for a random failure involves a single parameter, the failure rate
r. This gets derived at least empirically from the observation that if you have a pile
N of working components, then the observed failure rate goes as:
(EQ 1)
dN/dt = -rN
so the rate of loss relative to the number operational remains a constant throughout the aggregated lifetime of the parts. The solution to the differential equation is the classic damped exponential shown below:

Figure 1: The classical failure rate gives a damped exponential over time.
Now this works very effectively as a first-order approximation and you can do all sorts of reliability studies with this approximation. For example it matches the conditions of a Markov process, and the fact that it lacks memory means that one can solve large large sets of coupled equations (this has application in the
oil shock model, but that is another post).
Deviation from the Classical Premise: However, in reality the classic approximation doesn't always hold. As often observed, the failure rate of a component does not remain constant if measured empirically over a population. Instead the shape over time ends up looking something like a bathtub.

Figure 2: The Bathtub Curve showing frequent early failures and late failures.
One can see three different regimes over the life-cycle of a component. The component can either fail early on as a so-called "infant mortality", or it can fail later on randomly (as a lower probability event), or eventually as a process of wear-out. Together, the three regimes when pieced together form the shape of a bathtub curve. Curiously, a comprehensive theory for this aggregated behavior does not exist (some even claim that a unified theory is impossible) and the recommended practice suggests one create an analysis bathtub curve in precisely a piece-wise fashion. Then the analyst can predict how many spares one would need or how much money to spend on replacements for the product's life-cycle.
Although one can get by with that kind of heuristic, one would think that someone has unified a concept that
doesn't require a piece-wise approximation. As it turns out, I believe that no one has really solved the problem of deriving the bathtub curve simply because they haven't set up the correct premise with a corresponding set of assumptions.
The Dispersive Failure Premise: Instead of going directly to Equation 1, let's break the failure mechanism down into a pair of abstractions. First, recall the classic description of the irresistible force meeting the immovable object (
wiki). Let's presume the battle between the two describes the life-cycle of a component. In such a situation we have to contend with modeling the combination of the two effects, as eventually the irresistible force of wear and tear wins out over the seemingly immovable object as its integrity eventually breaks down. In other words, failure arises from a process governed by a time rate of change (of the irresistible force) which operates against a structure that maintains some sense of integrity of the component (the immovable object).
To set this up mathematically, consider the following figure. We scale the integrity of the component as a physical dimension; it could be a formally defined measure such as strain, but we leave it as an abstract length for the sake of argument. The process acting on this abstraction becomes a velocity; again this could be a real force, such as the real measure of stress. Now when something breaks down, the irresistible force has been applied for a certain length of time against the immovable object. The amount of time it takes to cover this distance is implicitly determined by the integral of the velocity over the time. However, due to the fact that real-life components are anything but homogeneous in both (1) their integrity and (2) the applied wear-and-tear, we have to apply probability distributions to their nominal values. Pictorially it looks like a range of velocities trying to reach the effective breakdown dimension over the course of time.

Figure 3: Abstraction for the time dependence of a failure occurrence.
Some of the trajectories will arrive sooner than others, some will arrive later, but a mean velocity will become apparent. This variation has an applicable model if we select an appropriate probability density function for the velocities, denoted by
p(v) (and justified later for the integrity of the structure, a corresponding
p(L)). Then we can devise a formula to describe what fraction of the velocities have not reached the "breakdown" length.
Probability of no breakdown as a function of time =
integral of p(v) over time for those velocities not reaching the critical length, L
For the maximum entropy PDF of
p(v)=alpha*exp(-alpha*v) this mathematically works out as
P(t) = 1-e-alpha*L/t
for a set of constant velocities probabilistically varying in sample space. This becomes essentially a dispersion of rates that we can apply to the statistical analysis of failure. If we then apply a maximum entropy PDF to the set of
L's to model randomness in the integrity of the structure
p(L) = beta*exp(-beta*L)
and integrate over
L, then we get
P(t) = 1-1/(1+alpha/(beta*t))

This has a hyperbolic envelope with time. The complement of the probability becomes the probability of failure over time. Note that the exponential distributions have disappeared from the original expression; this results from the alpha and beta densities effectively canceling each other out as the fractional term
alpha/beta. The
alpha is a 1/velocity constant while the
beta is a 1/length constant so the effective constant is a breakdown time constant,
tau=alpha/beta.
P(t) = 1-1/(1+tau/t)
The assumption with this curve is that the rate of the breakdown velocities remains constant over time. More generally, we replace the term
t with a parametric growth term
t -> g(t)
P(t) = 1-1/(1+tau/g(t))
If you think about the reality of a failure mode, we can conceivable suspend time and prevent the breakdown process from occurring just by adjusting the velocity frame. We can also speed up the process, via heating for example (as the popcorn example shows). Or we can imagine placing a working part in suspended animation, nothing can fail during this time so time essentially stands still. The two extreme modes roughly analogize to applying a fast forward or pause on a video.
A realistic growth term could look like the following figure. Initially, the growth proceeds linearly, as we want to pick up failures randomly due to the relentless pace of time. After a certain elapsed time we want to speed up the pace, either due to an accelerating breakdown due to temperature or some cascading internal effect due to wear-and-tear. The simplest approximation generates a linear term overcome by an exponential growth.

Figure 4: Accelerating growth function
or written out as:
g(t) = a*t + b*(ect -1)
This becomes a classic example of a parametric substitution, as we model the change of pace in time by a morphing growth function.
Now onto the bathtub curve. The failure rate is defined as the rate of change in cumulative probability of failure divided by the fraction of operational components left.
r(t) = -dP(t)/dt / P(t)
this results in the chain rule derivation
r(t) = dg(t)/dt / (tau + g(t))
for the
g(t) shown above, this becomes
r(t) = (a+b*c*ect) / (tau + a*t + b*(ect -1))

which looks like the bathtub curve to the right for a specific set of parameters,
a=1,
b=0.1,
c=0.1,
tau=10.0. The detailed shape will change for any other set but it will still maintain some sort of bathtub curvature. Now, one may suggest that we have too many adjustable parameters and with that many, we can fit any curve in the world. However, the terms
a,b,c have a collective effect and simply describe the rate of change as the process speeds up due to some specific physical phenomena. For the popcorn popping example, this represents the accelerated heating and subsequent breakdown of the popcorn kernels starting at time
t=0. The other term,
tau, represents the characteristic stochastic breakdown time in a dispersive universe. For a failed (i.e. popped) popcorn kernel, this represents a roll-up of the dispersive variability in the internal process characteristics of the starch as it pressurizes and the dispersive variability of the integrity of the popcorn shell at breakdown (i.e. popping point). We use the maximum entropy principle to estimate these variances since we have no extra insight to the quantitative extent of this variance. As a bottom-line for the popcorn exercise, these parameters do exist and have a physical basis and so we can obtain a workable model for the statistical physics. I can assert a similar process occurs for any bathtub curve one may come across, as one can propose a minimal set of canonical parameters necessary to describe the transition point between the linear increase and accelerated increase in the breakdown process.
The keen observer may ask: whatever happened to the classical constant failure rate approximation as described in Equation 1? No problem, as this actually drops out of the dispersion formulation if we set
b=tau and
a=0. This essentially says that the acceleration in the wear and tear process starts immediately and progresses as fast as the characteristic dispersion time
tau. This is truly a zero-order approximation useful to describe the average breakdown process of a component.
So the question remains,
and I seem to always have these questions; why hasn't this rather obvious explanation become the accepted derivation for the bathtub curve? I can find no reference to this kind of explanation in the literature; if you read "A Critical Look at the Bathtub Curve" by Klutke et al [1], from six years ago, you will find them throwing their hands up in the air in their attempt to understand the general bathtub-shaped profile.
Next, how does this relate to oil discovery? As I stated at the outset, a failure is essentially the flip-side of success. When we search for oil, we encounter initial successes around time=0 (think 1860). After that, as more and more people join the search process and we gain technological advances the accelerated search takes over. Eventually we find all the discoveries (i.e. failures) in a large region (or globally) and something approaching the classic logistic results. In this case, the initial downward slope of the oil discovery bathtub curve becomes swamped by the totality of the global search space. The mathematics of dispersive failures and the mathematics of dispersive discovery otherwise match identically. Thus you see how the popcorn popping statistical data looks a lot like the
Hubbert peak, albeit on a vastly different time scale.
As a side observation, a significant bathtub curve could exist in a small or moderately sized region. This may occur if the initial discovery search started linearly with time, with a persistent level of effort. If after a specific time, an accelerated search occurred the equivalent of a bathtub curve could conceivably occur. It would likely manifest itself as a secondary discovery peak in a region. So, in general, the smaller exploration regions show the initial declining part of the bathtub curve and the larger global regions show primarily the upswing in the latter part of the bathtub curve.
As I continue to find physical process that one can model with the dispersion formulation, I start to realize that this explains why people don't understand the bathtub curve ... and why they don't understand
popcorn popping times ... and why they don't understand
anomalous transport ... and why they don't understand
network TCP latencies ... and why they don't understand
reserve growth ... and why they don't understand fractals and the
Pareto law ... and finally why they don't understand
oil discovery. No one has actually stumbled on this relatively simple stochastic formulation (ever?). You would think someone would have discovered all the basic mathematical principles over the course of the years, but apparently this one has slipped through the cracks. For the time being I have this entire field to myself and will try to derive and correct other misunderstood analyses until someone decides to usurp the ideas (
like this one).
The finding in this post also has a greater significance beyond the oil paradigm. We need to embrace uncertainty, and start to value
resiliency [2]. Why must we accept products with
built-in obsolescense that break down way too soon? Why can't we take advantage of the understanding that we can glean from failure dispersion and try to make products that last longer? Conservation of products could become as important as conservation of energy, if as things play out according to a grand plan and oil continues to become more and more expensive.
References- Klutke, et al, "A Critical Look at the Bathtub Curve", IEEE Transactions on Reliability, Vol.53, No.1, 2003. [PDF]
- Resilience: the capacity to absorb shocks to the system without losing the ability to function. Can whole societies become resilient in the face of traumatic change? In April 2008 natural and social scientists from around the world gathered in Stockholm, Sweden for a first-ever global conference applying lessons from nature's resilience to human societies in the throes of unprecedented transition.