Bush hitting the everclear
If Bush gives ethanol the big push as predicted in tonight's SOTU address, that will provide the final nail in the coffin for ethanol's future. Has Bush gotten anything right yet?
| Imperialistic house of prayer, |
|
Conquistadors who took their share. |
If Bush gives ethanol the big push as predicted in tonight's SOTU address, that will provide the final nail in the coffin for ethanol's future. Has Bush gotten anything right yet?
In the last post, I hinted that the parabolic growth law that oil reserve growth estimates seem to follow will likely hit some hard limit. After all, no one really believes in an infinite supply of oil .. do they?
dG(t)/dt = D (C(0)-C(x))/G(t)

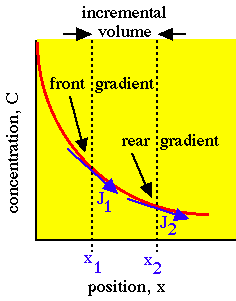 Not wanting to work out the second law, but sensing that the concentration changes with oil depletion, I worked out a modification to Fick's first law whereby I changed the C(x) term to track the growth term G(t). This basically says that over time, the concentration differences start to level out.
Not wanting to work out the second law, but sensing that the concentration changes with oil depletion, I worked out a modification to Fick's first law whereby I changed the C(x) term to track the growth term G(t). This basically says that over time, the concentration differences start to level out.dG(t)/dt = D (C(0)-a*G(t))/G(t)Unfortunately, one can't find an analytical solution to this equation (except for the asymptotic behavior, which drops out straightforwardly). But, alas, we do have computers to do the grunt work of numerical integration. The following curve results for an a/C(0) ratio of 0.09 (the asymptote rather nicely goes to 1/0.09=11.1).

In the USA, the government prohibits speculative estimates of the remaining oil in a field.
Operators in the United States are required by law to report only those reserves that are known with high certainty to be available for production, thus excluding resources that are at all speculative. It follows that one component of reserve growth is the difference between early estimates of recoverable resources, which in the presence of limited data are required to be conservative, and later estimates based on better knowledge of the field.This means that oilers can't use the reserve estimate outlined in the previous post. That technique, which empirically demonstrates a growth of 10x or more from the initial estimate after 90 years, apparently ranks as a speculative estimate (blue curve below, assuming an initial growth estimator of 0.1). So, instead of coming up with an estimate based on established heuristics, the field operators always undershoot the actual amount, to safely remain below the "speculative" point.

df(t)/dt = K/f(t) - C*f(t)I haven't checked the literature, but the parabolic growth law for oxidation should follow this behavior for very thin substrates where the source of materials limits out physically.
I looked at the dynamics of fossil fuel "reserve growth" some more and I do not think it demonstrates compound growth by any stretch of the imagination. If it did in fact show such behavior, the growth would fly off the chart in a Ponzi scheme fashion.

dF/dt = k/F(t)Note that the fractional rate reduces to:
F = sqrt (2kt)
dF/dt / F = 0.5/tNote that this follows the "reserve growth" curve fit fairly well, where the fractional growth rate slows down inversely proportional to time. Microelectronics engineers refer to this as the parabolic growth law (a parabola sitting on its side, see the overlay on the green curve below).

At the urging of a petroleum engineer at the PeakOil.com board, I took a look at the Attanasi & Root approach to predicting reserve growth. I grabbed the oil field data from the journal below and OCR'd into something I could analyze (raw data here).
"Attanasi, E.D., and Root, D.H., 1994, The enigma of oil and gas field growth: American Association of Petroleum Geologists Bulletin, v. 78, no. 3, p. 321-332."

This narrative describes the virtual flow of oil through the system from discovery to production, providing a problem domain description to how an oil peak occurs. You can find the accompanying stochastic differential equations here.

dP/dt = K * (t0-t) * P(t)
t0=PeakTime. This relationship reads that the production increase slows down over time linearly, but also scaled by the amount in production at that time -- kind of an linearly decreasing positive feedback turned into a linearly increasing negative feedback. At t=t0, the production increase turns into a production decrease. Unfortunately, I can't provide a problem-domain narrative for the gaussian formulation. Like the logistic curve formulation, I get brain-freeze trying to shape it into intuitive terms.
We live in a stochastic world. The best prediction you can make with only minimal prior knowledge takes into account only the currently occupied state. That basically captures the essence of a first-order Markov process or property, which can describe the salient effects of many different phenomenon, everything from random walk to oil depletion. The process involves lots of little stepped events that collectively accumulate in a fuzzified fashion. It inexorably leads you in a direction, but the direction remains governed by largely randomly distributed events.

Markovian Process (Graffin)
You will all say that I am surely crazy
Only an unrepentant pessimist whose thoughts should be detained
But facts are sterile, not vulgar nor sublime
And they're not religion, they're for everyone
And signify the times
Today is a window, tomorrow the landscape
All you need to do is take a look outside
To know what we're bound to face
The level of disparity
The common man
The manner of destruction of the native land
The poverty of reprisal from all involved
And the scathing trajectory from the past
Markovian process lead us not in vain
Prove to our descendants what we did to them
Then make us go away
I live in an urban area, so you would think I would have an easier time getting around via pedestrian or bike power. Well, yes and no. I certainly have a number of roads to use and choose from; however, I run into enough man-made and natural obstacles to make navigation more difficult than it ordinarily should.

Through some straightforward math, I can create a closed-form expression for the stationary solution to the oil shock model. Note that this assumes constant values for all associated rates over time and a delta value for the discovery term. As a sanity check, the solution matches that of the gamma function in the special case of equivalent rates assumed during each phase.
F(t) = Discovery stimulus
R1(t) = Reserve emerging from fallow state, Rate = a
R2(t) = Reserve emerging from construction state, Rate = b
R3(t) = Reserve emerging from maturation state, Rate = c
R(t) = Reserve emerging from production state, Rate = d
P(t) = Production curve
dR1/dt = F(t) - a*R1(t)
dR2/dt = R1(t) - b*R2(t)
dR3/dt = R2(t) - c*R3(t)
dR/dt = R3(t) - d*R(t)
P(t) = d*R(t)
r1(s) = f(s)/(s+a)If we assume a single delta for discoveries, then
r2(s) = a*r1(s)/(s+b)
r3(s) = b*r2(s)/(s+c)
r(s) = c*r3(s)/(s+d)
p(s) = f(s)*a*b*c*d/(s+a)/(s+b)/(s+c)/(s+d)
f(s)=1. The inverse Laplace transform gives the following (unscaled) time-domain expression

--Update: A Pilgrim's Progress--
This helium-filled contraption may have a shorter life-span than the Hindenburg.

"By Zeppelin to Muncie"
A commenter at PeakOil.com referenced a paper on the "enigma" of reserve growth. I assume they call this an enigmatic phenomena in that no one really understands reserve growth and why it occurs. I have a few ideas, but first note a couple of things from the article. The authors work as consultants and hail from Canada. Does this color their outlook? Let's look at the charts. The first one shows a growth that appears fairly significant, perhaps an order-of-magnitude effect on reserve growth for oil and gas. However the second and third chart shows much more moderate growth.



ReserveGrowthRulz wrote:In comparison to what? The orangutan race? The Martian race?
Oh...I never said that ALL civilizations made the transition down through the ages from one energy form to another, just that us, as the human race, has done better in general, and succeeded in general, as we progressed through time and technologies.
The technique of Hubbert linearization for estimating oil URR works perfectly for only one class of models: those which obey the logistic curve. Although a linearization technique may apply for other models, the fact that no one uses other models likely means that one does not exist -- as of yet.


_files/image008.gif)
Finally, Campbell and Laherrere use production data to estimate field size, "improving" on the IHS Energy data. By graphing production against cumulative production, as in Figure 3, they claim that a clear asymptote can be seen, allowing for a more accurate estimate of ultimate recovery from the field. The first problem with this is that there is no explanation for how often the method is employed.I see the problem in that Lynch does not plot the curve in the classical Hubbert sense, i.e. he forgets to divide production by cumulative along the vertical-axis. So basically, once again, either (1) Lynch gets something horribly wrong, or (2) the traditional analysts have become lazy in not rigorously using the Hubbert linearization, forcing Lynch to call them on it. Somebody may yet sort this out.
[...]
Examining this data does confirm that some fields display a clear-cut asymptote. However, out of 21 fields whose peak production was above 2 mt/yr (or 40 tb/d), only 7 show such behavior. The rest do not show a clear asymptote (as in Figure 4), or worse, show a false one, as Figure 5 indicates. Clearly, this method is not reliable for estimating field size.


Now, take a look at some of the other curves in Lynch's paper:_files/image006.gif)
Kind of spooky? Look at the superposition of the curves.

rockdoc123 wrote:I responded:Quote (me):having a black helicopter tin foil kind of day are we? There is reams of views on what is left to be found in the literature, has been since the seventies. Check American Association of Petroleum Geologists Bulletin, Bulletin of Canadian Petroleum Geology, Petroleum Geology, USGS Energy group assessment, etc.
And will this get out to the textbooks? Or will it get buried like the rest of the stuff, until we all say "Wha' Happ'n?
Compared to the clueless petroleum engineer featured in yesterday's post, the geologist rockdoc takes a measured view of things. He remains optimistic and offered up some thoughts on my depletion modeling approach here. However, I still get frustrated because of the casually dismissive attitude that big oil has apparently indoctrinated into anyone that gets within a 10-ft pole distance of their clutches. I annotated his musings with my own rhetorical questions in the following snippet:
rockdoc123 wrote:So why did not such a fundamental analysis get transferred to the textbooks? The lack of this kind of analysis is much like teaching first-year electrical engineering without introducing Kirchoff's Law. It's just freaking rate equations and conservation of matter. This to me is deeply troubling. I didn't take an earth sciences major, but I have taken classes in subjects such as limnology and the first thing you learn is that all freshwater lakes go through a life-cycle, birth through death. Are the petroleum engineering departments so vain and self-conscious not to even broach the subject of the life-cycle of oil? To avoid teaching that the whole thing is just a house of cards or a ponzi scheme, certain to eventually collapse, strikes me a bit irresponsible.
WebHubbleTelescope...what you just created as I remember was being used some twenty years ago in the research labs (back when oil companies like Gulf and Shell had large research facilities and had no problem hiring people with a maths jones to sit in an office and fiddle with data).rockdoc123 wrote:And will this get out to the textbooks? Or will it get buried like the rest of the stuff, until we all say "Wha' Happ'n?"
Today most oil companies are just not that interested in how much might be left overall (exception would be BP who still has a pretty big research component)...they spend their time modeling existing production and coming up with predictions on whats left to be discovered in various parts of the world where they are working.rockdoc123 wrote:OK, so this got published. How about the results from 20 years ago?
This sort of analysis involves more subsurface information and requires less math analysis of past trends. If memory serves me correctly some of the old analyses were published in the AAPG Bulletin.rockdoc123 wrote:I have analyses for North Sea, World, lower-48, even for natural gas.World | Lower-48 | UK North Sea | Former Soviet Union | New Zealand NG | Norway
It would be interesting to look at the same analysis for somewhere other than the US.
I use the same model for everything, vary the parameters a bit, and gain an understanding that I surely would not have if these rate equations were not available. We could be mining for marbles, it doesn't really matter, I see no fundamentals being taught or published anywhere. The more I look at it, this stuff with the Logistic curve and Gaussian fitting is basically rubbish. It's equivalent for me to trying to teach the response of analog electric circuits by looking at the output waveform. I would like to see the oil depletion modeling rise a step above shear empiricism.rockdoc123 wrote:Government-imposed obstacles seem like a second-order effect when put up against the greed of the human animal. Teach the first-order effects first. Just about everything in engineering is first -order effects. If you don't do the first-order stuff first, you should just give up. They don't call it first-order for nothing.
Arguably the US has been a poster child for making discoveries and getting them on-stream with little in the way of interuption or government imposed obstacles.
Over at peakoil.com, someone posing as a petroleum engineer made this rather optimistic claim:
ReserveGrowthRulz wrote:Upon which, I responded:
Depletion alone is only a part of the overall dynamics which go into worldwide production rate, without accounting for new discoveries, their sizes and future rates, old fields changing their depletion profile through better technology and reserve growth, new areas opening up to exploration as, say, the Arctic seapack melts and makes more areas available, without including all of these it would seem to me depletion modeling exclusively is kinda like closing your eyes, grabbing an elephant by the tail and trying to describe his size off of what you've got in your hand?
Using the melting Arctic seapack as a rationalization for anything strikes me as a last gasp attempt at maintaining the status quo.
Cripes, if the seapack starts to melt at rates at which we need to replenish our oil supply we have a whole "boatload" of problems to start worrying about.
Arctic ice melting opens up areas of exploration that haven't been available before, both practically and economically. The USGS numbers for undiscovered resources for Greenland are a perfect example, they say maybe there is a little, but maybe there is ALOT.
One of peak-oil denier Michael Lynch's favorite arguments to counter the oil depletion pessimists out there (Campbell and Laherrere, et al) has to do with questionable interpretation of the so-called "creaming curves" from mature fields. Since I did some real honest-to-goodness Monte Carlo simulations fairly recently, I think I have a handle on what Lynch has gone half-cocked over. Bottom-line: nothing to get excited about -- just Lynch practicing his highly refined art of attacking the model and not the reality of the situation.
_files/image004.gif)
_files/image002.gif)
In my previous post, I made an offhand reference to how the initial increase of crude oil discoveries might follow a certain well-understood pattern:
I then put a "gold rush" mentality on the frequency of discovery strikes; this essentially started with 8 strikes per year and rising to 280 strikes per year at the peak.You can either think of the discovery growth as a steady year-to-year increase or as an accelerating increase.
 The latter refers to a quadratic growth law commonly found in many situations where increasing numbers of resources get applied to a problem over time. Much like gold spawns a fevered rush of interest which seems to accelerate through a parabolic boom before finally busting, I offer that oil strikes might follow the same swarming pattern.
The latter refers to a quadratic growth law commonly found in many situations where increasing numbers of resources get applied to a problem over time. Much like gold spawns a fevered rush of interest which seems to accelerate through a parabolic boom before finally busting, I offer that oil strikes might follow the same swarming pattern.
Quadratic Growth :d2Q(t)/dt2 = k
Exponential Growth :dQ(t)/dt = aQ(t)



On a brilliant Saturday afternoon, August 27, at 69 feet down, the drill suddenly dropped six inches into a crevice. Uncle Billy fished it out, wiped it off carefully, and knocked off for the Sabbath. But Monday seemed a long way off, and on Sunday Smith was back at the well, peering down the pipe, wondering if he really saw something glistening on the surface below. He grabbed a leftover end of pipe, plugged it up like a dipper, and thrust it down on a stick. It came back up filled to the brim with oil. A wild shout brought several mill hands running. Young Sammy raced off to town to notify Colonel Drake.The story also gives some older historical background. I did not know this, but arguably, we shouldn't even attach the discovery of oil in Titusville to any individual person. Many settlers had seen the residue in the oil over the years. So yes, in fact, it likely showed a fallow period, followed by Drake's construction period, and finally a maturation period.
The whole village was buzzing; even townsmen who still couldn't imagine what might come of the find were eager to see it. A man from the nearby town of Franklin, on the Allegheny River, who visited Drake's well the following day, joining the eager crowds streaming in on every road in wagons, on horseback, and on foot, reported, "It comes out a flowing dark grease with a heavy white froth."
By then, the few pine barrels Drake had provided were already full. Drake took Margaret Smith's washtub from the engine-house shanty (she complained later she never could get it clean after that), then commandeered old whiskey barrels and sperm oil containers. And still Uncle Billy kept pumping and the oil kept coming; so did the crowds.
I learned moons ago in engineering school that you should not fear noise. Noise can actually tell you a lot about the underlying physical character of a system under study. I started thinking about this again because of the historically noisy oil discovery curves that get published. This chart of global discoveries appears unfiltered:


"Pearson's r" test found no correlation between oil discoveries from one year to the next, i.e. discoveries appear to be random.The fluctuations become very apparent because of the limited number of discoveries we have had in a finite amount of time. Laherrere estimates that worldwide we have had on the order of 10,000 crude oil discoveries. Pepper this over a range of 100 years and you get a relatively small sample size to deal with per year. This small number over a span of <100 years essentially gives rise to the relatively big yearly fluctuations. Making it even worse, we still have to consider the distribution of resorvoir sizes; anything that shows a large variance in sizes (i.e. a spread) will lead to larger fluctuations.
Lognormal distributions -- a method based on the observation that, in large well-explored basins, field-size distributions approximate to a lognormal distribution. The method is most reliable with large datasets, i.e., in mature basins, and may be unreliable with small datasets.As the variance tightens around the mean, the shape of the curve peaks away from zero. But importantly, a large variance allows the larger-than-average sizes (the "super-giants") to appear.

The area under the complete discoveries curve must equal the area under the eventually completed global production curve, whatever it's math description - oil discovered must equal oil produced. The discovery process is controlled heavily by the math laws of probability with the bigger, easy-to-find pools of oil found first. Resource discoveries fall on bell curves too. Deffeyes makes the point that even with changing technology, this is the way discoveries play out. The global discoveries curve peaked in the mid 60s and, despite the immense tech revolution since then, the charted yearly discoveries have formed a pretty nice fit to a Gaussian bell curve, particularly if they are "smoothed" by grouping into 5 year bars in a bar graph.I decided to take a shot at running a Monte Carlo analysis that shows the natural statistical fluctuations which occur in yearly discoveries. This data comes from several Monte Carlo trial runs of 10,000 samples with a log mean of 16 (corresponding to 9 million barrel discovery), and a log standard deviation (corresponding to 0.73 million barrel on the low side and 108 million on the high side). I then put a "gold rush" mentality on the frequency of discovery strikes; this essentially started with 8 strikes per year and rising to 280 strikes per year at the peak.






Remember that the Megagiant field size sits on the 99 percentile of world field size distribution….meaning that the chance of finding another is pretty slim.The RockDoc, an industry insider, promises to provide some data after I maniacally ask "I propose that rockdoc volunteer what he thinks is the global log-normal distribution of discovery sizes".
As to the likelihood of finding more of them diminishing every day….that is only true if exploration efforts in areas where they are most likely to be found has been aggressive.
I think I can do that...I have a nifty program that will plot out field size on log normal probability paper. May take some time to dig up the field sizes though (I think I have it up to 2003 but may not have the 2004 data yet)....I'll first check to see what is in print already. There are some problems in doing this though...as an example Ghawar is often treated as being one big accumulation when in fact there are several distinct pools...hopefully that will be lost in the noise.We'll see what he comes up with. He better get it out quick before every single internet transmission gets filtered by corporate legal departments courtesy of BushCo.
Staniford has a new Hubbert Linearization post up at TOD. I still don't feel that approach merits any worth, but many people feel differently; from a commenter at the site:
It doesn't seem to be out of the realm for this to be taught in college/grad school to a fairly broad audience. Why has this been held back so long?I can answer that. Because this particular approach resorts to a grab-bag of heuristics and empirical relationships and does not rise far above mere fortuity. Staniford says hisself that
" (I confess that I still don't fully understand why this model works as well as it seems to in practice)"Placing myself in such a situation, I wouldn't feel comfortable teaching anything I don't deeply understand to a bunch of hungry graduate students. On the other hand, I would feel perfectly fine teaching the oil shock model, because of its reliance on some physical reality and the properties of stochastic processes.
I think Kevin Drum set up his readers with this post regarding a solution to global warming, caused by decomposing agricultural waste:
Take advantage of that. The leftover corn cobs and stalks from our fields can be gathered up, floated down the Mississippi, and dropped into the ocean, sequestering it. Below about a kilometer depth, beneath a layer called the thermocline, nothing gets mixed back into the air for a thousand years or more. It's not a forever solution, but it would buy us and our descendents time to find such answers. And it is inexpensive; cost matters.The catch, as succintly revealed in the comments:
corn cobs float
I gave a shot at modeling the Norway depletion curves starting from the Laherrere discovery data.

Unshocked -- 10%
Shocked -- 10% to 20%

 Note how close the profile of the shock perturbation approaches that of the UK North Sea model (chart to the right). In both cases, the increases in extraction rate occurred right around 1992, and essentially targeted the same 3 MBls/day sustainable production rate (competitive pressures perhaps?).
Note how close the profile of the shock perturbation approaches that of the UK North Sea model (chart to the right). In both cases, the increases in extraction rate occurred right around 1992, and essentially targeted the same 3 MBls/day sustainable production rate (competitive pressures perhaps?).
If media reaction serves as an indicator of the outrage, I would presume that we will soon hear "more strip mining" as a safer alternative to coal mining. I predict the first talking points will come out of the Druggie Limbaugh show. His favorite whipping boys, the "eco-nazis" will become the target of blame for what happened in West Virginia.
One day in and I have broken my resolution. This unsubstantiated quote by OILYROD follows up on a PeakOil.com message from last year in reference to the inventor of the SkyCar:
Not surprising, considering his over-the-top resume.
PostPosted: Wed Jan 04, 2006 7:41 am
Post subject: Re: Professor Paul Moller: Peak oil is a F#$%ing scam!
As a long time former employee of Dr Moller (AKA PT Barnum)I would like to set the record strainght.
1. He is not a professor at UC Davis, and hasn't been for over 15 years. He was never professer emeretus of anything.
2. He is in the business of taking peoples money, that's all. Shit, Burt Rutan got a plane into SPACE (twice) for about 20 mil. Where do you think PT has put the 50 to 100 mil he's duped folks out of?
3. The technology is impractical, and Mollers vehicles just don't work. The last test flight (30 sec and 15 feet up) was almost 3 years ago.
4. Moller has been making claims like today's for about 30 years. It's always "just around the corner". Google his name or "Discojet" and see what you come up with.
5. The only thing this guy is expert att is taking other peoples money.
When he was only 6 years old he began construction of his first house.He likely obtained several technical degrees in utero as well.
I heard a spirited, yet civil, exchange on the Majority Report radio show on AAR tonight. The show featured a discussion between John Perkins (author of "Confessions of an Economic Hit-Man"), the hosts Janeane Garafalo and Sam Seder, and Janeane's father Carmine, who happens to have worked at Exxon in some capacity for the last 30 years. Carmine, somewhat of a staunch republican, apparently doesn't buy into the premise for Syriana, the depiction of oil executives thereof, the reasons for entering Iraq, etc. Janeane summed it up by saying something along the lines of "some people just don't want to know the truth, as it disrupts their belief system". For me, I still don't know whether Perkins plays up the snake-oil a bit too much, but nothing lately has negated any of his assertions. Perkins thinks the Iraq/euro connection created one rationalization for invading, yet Stirling Newberry thinks otherwise:
Fears about the US dollar - or about oil trading in Euros, are however, overblown. Instead, instability will help the dollar, as "flight to safety" will drive risk averse parked money here to the US. It doesn't matter what oil is traded in - the pound crumbled in the 1920's even though it was the unit of account for major commodities - but instead where the money is parked afterwards. Trading in euros will give Iran and other nations a hedge against another move on the dollar, but this is not significant. What is more significant is that there is a sharp willingness on the part of major dollar holders to move to Euro based stocks and bonds. The trigger point will be a European recovery. If europe can recover from its current economic slump, and raise rates, this will be a capital magnet. There are those that worry that this is destined to happen soon. However, the likelihood is that it will not happen until late in 2006 or early 2007, which means that the pressure on the greenback is still two years away.Of which Perkins acknowledged as well, in the context of China thirst for oil and their reliance on Iraq/Iran oil.
The real tinderbox is not mechanisms, but control over the oil itself, and US attempts to keep nations that are oil holders vulnerable to US military pressure. ...
Three Kings (1999)
George Clooney's character: "I don't even know why we're [in the Middle East]."
character Ron Horn: "Don't start that with me."
Clooney: "Just tell me what we did here, Ron."
Ron: "What do you want to do- occupy Iraq- the new Vietnam all over? Is that your brilliant idea?"
Pi (1998)
Sol Robeson: "This is insanity, Max."
Maximillian Cohen: "Or maybe it's genius."
I had a chance to get some extra cross-country skiing in during the holiday break and came away with a sour taste from the decision making of the local parks and recreation board. A local park reserve called Elm Creek recently underwent "renovations" that amounted to lots of earth-moving activity. Most of the changes centered around the upgraded visitor center and I came away perplexed that I really didn't recognize the landscape that I had gotten used to over the last dozen or so years that I have visited the reserve. In particular I noticed a massive clearcutting of foliage on the main slope running down from the center to apparently make room for multiple grooved sledding runs. To me it looked more like a moonscape or a Fred Freakin Flintstone RV park.
Bush showed reporters an injury to his forehead, a scrape from "combat with a Cedar" while brush-clearing at his ranch. "I eventually won. The Cedar gave me a little scratch," he said.Won what? The battle? Or the war?
So he clears brush like a madman everytime he gets the chance, hiding behind his Oakley's, blessedly unable to hear anything over the sound of chainsaws ---- maybe even the voices inside his head that remind him that he's still got three more years of this horrible responsibility he knows he cannot handle.