In a pending post to
TheOilDrum.com, I make an analogy of oil reserve dispersive discovery to the results of a competitive foot-race such as the marathon. In this post, I take actual data from a couple of marathons and demonstrate quantitatively how a comparable dispersion occurs. Not knowing ahead of time whether the analogy had a basis beyond that of strong intuition, it surprised me that it gives such a remarkably good fit. I consider this great news in that it gives readers and lay-people significant insight into understanding how the dispersive discovery plays out in a more intuitive domain area. After all, everyone understands how competitive sports work, and a foot race has to rate as the simplest sport ever concocted.
And if they don't appreciate sports, we can always equate race results to oil businesses seeking fastest time-to-market.
The analogy of a marathon to dispersive discovery holds true in a specific situation (which we can later generalize). First, consider that the goal of the marathon lies in reaching (i.e. finding) the finish line in the shortest possible time. We make that the goal of the whole group of runners -- to achieve a minimum collective finish time. To spice things up we place pots-of-gold at the finish line -- so they essentially race to find the resource. For dispersive discovery, the goal becomes finding the oil buried in the ground by sending out a group of exploratory prospectors. The "seam" of oil below ground becomes the finish line, and the prospectors act as the runners.
The premise of dispersive discovery assumes that the prospectors have differing abilities in their speed of reaching the seam. In a large citizen's marathon, we definitely find a huge range in abilities. The spread in the distribution turns out rather large because humans have different natural abilities and more importantly, show different levels of dedication in training. Our inherent human laziness and procrastination say that the mode of the distribution would tilt toward the "low-speed" runners. Look at the following figure and imagine that the speed of the runners show a histogram distribution that leans top-heavy to the slowest of the runners.

The specific distribution shown, that of a damped exponential, has the interesting property that it has a standard deviation equal to the mean. This historically has resulted in a safe and conservative approximation for many real processes. The mode (most commonly occurring value) gives the laziest possible speed (nearing zero) and the least common gives the maximum training exertion. The distribution always has a bounded mean.
I used data from the Hawaii Marathon (also a leg of the Ironman Triathlon) to fit this dispersion model to. The Hawaii race has some
interesting characteristics: it has a huge number of participants, it has no course closing or cut-off time (thus encouraging slow runners to compete), and it has a relatively small elite field. Lots of Japanese citizens enter the race. To make it more homogeneous, I decided to use only the female entrants.
I used
on-line data for the finish times. The "seam"-based dispersive discovery has a simple equation
N = No exp(-T/t), where
N0 is the total number of finishers and
N is the cumulative number at finish time
t. The parameter
T gives the dispersive spread. I believe the key to implementing the model correctly revolves around the premise of establishing a maximum possible speed that the runners can not humanly exceed, which equates to a minimum finishing time
T0. The dispersed speeds become virtual speeds proportional to
L/(t-T0). So for the equation, for convenience, we establish these artificial starting points and measure
t from that new origin.
The figure below consists of over 10,000 female finishers shown by the dark line. Note that even though no official cut-off exists, the curve starts to break horizontally at 8 hours; most people consider this a natural cut-off as the human mind and body starts to get beaten down over that length of time. The model fit works very well, apart from the diverging above the natural cutoff time of 8 hours. (The dispersion eventually reaches an asymptote of 35,000)

The logarithmic plot shows an even more interesting feature. Note the bulge in the curve at early finish times. This, I contend, results from the introduction of a small elite field of competitors (perhaps 30) to the race. These elite women have greater athletic capabilities and have the carrot of prize money to justify separating the model into two components. Note however that on a linear plot, this bulge gets buried into the noise, and the statistics of the much larger mortal citizen racers takes over.

The following figure shows the histogram of the speeds for the women finishers of the Hawaii Traithlon. Plotted on a log axis, the straight line indicates that it matches the damped exponential of the assumed speed distribution. Note that very low speeds do not occur because of the natural cut-off time.

The chart below shows the R2 of the histogram for the aligned part of the model. This slope matches precisely to the eyeball fit of the cumulative finish time plot in the first figure. To get an exponential fit, I censored the data by removing the points beyond the flattened 8 hour cut-off point.

We eventually have to understand why the very slowest speeds do not occur in a competitive race. The "inverse" of the histogram, shown below plotted in time space, clearly demonstrates the lack of long finish times.

I think I can understand this just from considering the segment of the population that wishes to run a marathon. Clearly anyone who runs a marathon has some level of fitness, which means that we naturally censor the entries to those who believe they can finish without embarrassing themselves. But we also know that a significant fraction of the population has a substandard level of fitness, either from obesity, general disinterest, or various health reasons; this segment essentially comprises the tail we would normally see on a finish-time results distribution,
if those non-athletes entered the race. This turns into a moot point because we will never force those people to run a race against their will. On the other hand, the oil discovery business shows no such constraint, as market capitalists will take as long as they need to get the job done, if money sits at the end of the rainbow.
As another example, the
Portland Marathon has no prize money for the elite field and favors very slow runners, even so far as encouraging walkers (a quarter of the entrants). The size of the women's field exceeds that of the men's by quite a bit. No cut-off exists but the race officials reduce the support at 8 hours. In the figure below, you can see that the red line shows a definite break at 8 hours as the
runners try to make it within that time (you have to set some personal goals after all).

Again the fit to dispersive discovery looks quite good over the non-censored range, especially for the female racers. The linear and log plots shown below demonstrate the same bulge for a small elite field. (The dispersion model eventually reaches an asymptote of 6100)

Portland has a much tighter dispersion than the Hawaii marathon. Even though Portland has around a third the participants as Hawaii, it finishes just as many runners within 4 hours. The prize money for Hawaii attracts a faster group of elite runners, but the average pace of Portland runners exceeds that of Hawaii by about an hour faster over the entire course.

A histogram of the rates shows the same damped exponential distribution, reinforcing the reason for the good model fit. Notice that the histogram has an even more exponential look than the Hawaii Triathlon. Since the Portland Marathon contains a huge number of female walkers (more so proportionally than Hawaii), the effect of censoring beyond the cut-off point becomes reduced even further. Again, one can ultimately imagine that if more couch potatoes who dream of finishing a marathon (a huge, huge number!) eventually entered, that the censored region would likely get populated, or at least fleshed out. They may have to resort to crawling (or a pub crawl) to finish, but that is what the statistics of the damped exponential tells us.

The model (and the whole analogy) works because all the runners desperately want to finish the race and thus they try as hard as they can to the best of their abilities. The same thing happens with oil exploration companies -- they will try as hard as they can to find the oil, since the potential payoff looms so large. The cumulative results of a marathon race look a lot like a discovery creaming curve, with the same "cut-off" feature. At some point, runners might decide that they can't possibly finish as they realize even walking slowly takes a toll. By the same token, the creaming curve often shows a similar horizontal cut-off asymptote whereby the oil company decides to stop further exploration as it takes a longer and longer time to find the oil at the slower rates. But as oil remains a tantalizing treasure, intrepid prospectors will keep trying and eventually break through any artificial cut-off.
This characteristic cumulative growth shape becomes the key rational for using the dispersive discovery model. Specifically,
note how well this formulation can work as a predictor. We can always measure the characteristic slope
early in the life-cycle and then extrapolate this simple curve to anticipate what the ultimate discovery will climb to. For marathon times, I can take a look at a fraction of the early finishers and anticipate when the rest of the field will finish. That measure alone determines the worth of a good predictor.
After finishing this analysis, I decided to look at the academic sports literature for a similar analysis. This paper
The “Fair” Triathlon: Equating Standard Deviations Using Bayesian Nonlinear Models, by Curtis, Fellingham, and Reese takes a scientific approach and treads some of the same territory that I explored. Interestingly, they did not look at distributions of rates to model finishing time statistics. Rather, they decided to use the times themselves and tried to fit these to a log-normal distribution. In the time domain, the profiles look like the following:

This approach has the problem of no justification; they basically pulled the log-normal out of thin air. It looks reasonable so they use it, whereas in the dispersive discovery we actually
model the behavior of the participants and then
mathematically solve the model. Further, to homogenize the populations, it also makes sense to separate the males and females. Fascinating that they didn't use this simple recipe, and from the references apparently no one else does either. I double checked with a
10K race (a component of the sprint tri) and see that shorter races also do not promote long finishing time tails. Psychologically, I don't think many people want to finish last, and worse yet, well behind the bulk of the pack.
In summary, I suppose I could do a few things to inferentially prove that a long "reserve growth"-like tail exists for marathon races. One could look at health records and figure out which segment of the population has a fitness level inappropriate for running a marathon and seeing if this fraction would hypothetically fill in the missing bulk.
WikiAnswers does not know the answer. Having run several marathons and tri's myself, I tend to believe that
"You should be able to have a fitness level of running up to 6 miles consistently". Whatever the case the missing tail accounts for around 1/3 a sampled population and perhaps over 2/3 according to the asymptotes for the Portland and Hawaii marathons respectively. This makes sense in that finishing a marathon race should pragmatically be accessible to around half the population, otherwise it wouldn't have the
popularity it has historically enjoyed, where perhaps 3-4% of Americans participate.
Once again, we find that all of sports gets reduced to probability and statistics. I knew that obsessively studying baseball card stats as a youth would eventually pay off.

















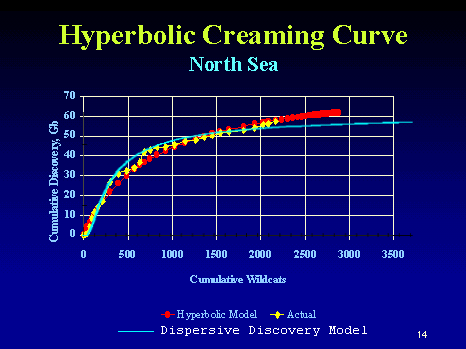
 BTW, I like HuffPo for everything else it does and love the regular posts by Steven Weber and Harry Shearer and the occasional gems from David Rees.
BTW, I like HuffPo for everything else it does and love the regular posts by Steven Weber and Harry Shearer and the occasional gems from David Rees.








