URR of Discovery/Shock Model

Some commenters on the last post asked about the seemingly large number I selected for a discovery URR of 3.43 trillion barrels. This overshoots the generally accepted number bandied about of 2.1 to 2.6 up to numbers as high as 3.345 trillion barrels according to a USGS estimate. So if anything, the Discovery/Shock model overshoots the low end wildly and the USGS estimate only slightly.

I think I can explain the reason for the discrepancy from the lower pessimistic estimates. Most of the numbers in the 2 to 3 trillion range come about from Hubbert Linearization estimates taken as we near the peak.

That takes it closer to the 2.1 to 2.3 trillion barrels normally quoted by Peak Oil experts than the 3 trillion expected by more optimistic analysts.

However, since HL does rely on a symmetric profile, out year data becomes inconsequential. You can see this if I try to do a Hubbert Linearization of the Discovery/Shock model data (actually the Discovery part only):

The red line extrapolation near the "halfway" point puts the URR at a little less than 2.6 trillion but the "hockey stick" or "dog leg" up pushes the actual URR out to 3.4. Note that this purely reflects the discovery model, which shows long tails caused by the apparent reserve growth discoveries.

To answer another question: in the previous post, I fit to the data set shown in this figure that Khebab posted at TOD, solving for CumulativeDiscoveries(2005) - CumulativeDiscoveries(1945) = D(2005) - D(1945), which gave me the 3.4 trillion.

Now that I see how close I am to the USGS estimates, and knowing how overly optimistically many analysts treat their interpretation, I get a little worried on the veracity of my own estimates. But then again we have to recall that the long tails have absolutely no impact on hitting a peak at this instant; it can only serve to delay the downturn if we can crank up the extraction rate. But does the proverbial world have the technical and political wherewithal to accomplish that? ... or do we instead choose a soft landing?

Discovery/Shock model

To recap, what do we know at this point?

A) We know that oil exploration efficiency has progressively improved over time; every year we critically evaluate bigger and bigger swaths though the earth's crust, looking for new deposits of oil. Unfortunately, the peak discovery years likely occurred during the early 1960's and we have since started exploring the fringes of oil's geological range. This has contributed to a monotonically diminishing rate of discovery, albeit somewhat mitigated by reserve growth.

B) We also know that once we discover a new reservoir of oil, it takes a while to start pumping and then to pump it dry. We obviously have to consider that some period elapses as the region sits fallow, that some period elapses as extraction facilities get constructed, and that some period elapses as the new rigs come online and reach maximum production. These three factors have some average value that we can make an educated guess at. We can also guess at an average extraction rate that works out proportional to the amount of reserve that we have left. This extraction rate, more than anything else, responds fairly quickly and agilely to market and political considerations.

C) We know that a good discovery model should help us quantitatively describe (A) and that a good extraction model should help us describe the dynamics of (B). With some work, we have arrived at a unified Discovery/Shock model which captures this knowledge mathematically.

Qualitatively we have this set of parameters:

• Discoveries first started in 1858 (the year t=0)
• Swept volume increase per year = k*t³
• Total volume and fraction containing oil = fV₀ = D0
• Fallow period = 5 years
• Construction period = 5 years
• Maturation period = 5 years
• Extraction rate = ?

We fit estimated global discovery curves and global production profile to this limited set of unknowns given the premise of a cubic-trend discovery model and a rate driven extraction model.

Khebab posted a discovery profile that demonstrates how backdating affects the historical record. Basically, much like what happens with economic metrics, what gets reported today may grow in the future.

We can clearly make out a peak in the early 1960's. We compare it to the well-known smoothed discovery profile superimposed on an oil production curve popularized by Laherrere.

I fit a yearly discovery model to Khebab's backdated data assuming a cubic growth model of constrained limit 3430 billion barrels (D0) and an acceleration term of 0.033 (k).

dD/dt = 4kt3*(1-exp(-D0/kt4)*(1+D0/kt4))

The green curve below shows discovery growth and decline superimposed on the non-backdated data in red. Note that reserve growth will conservatively fill in the tails to the right of the peak according to the model.

For the shock model production curve, I applied the discovery model as stimulus and used the perturbations in the extraction rate as shown below.

The blue and black curves suggest two possible future trends, a status quo on extraction rate starting at year 2005 that leads to an immediate decline or a monotonic increase in extraction rate that will stretch the peak out slightly beyond the 2020 time frame. In the past I had used extraction rates approximately double those shown, but I had little insight into a discovery model at the time that could predict potential in reserve growth nor did I have a straw-man extrapolated curve from pre-war discoveries. The extra cushion provided by a gradual modification of extraction rate makes me believe that we could keep up an undulating plateau for several years. In fact, just by increasing the extraction rate linearly to 0.035 until 2050, we could likely achieve a plateau until 2025 and a faster decline thereafter. This always boils down to the adage "pay me now or pay me later"; whatever extra production we can get now eventually comes back to bite us as a steeper decline on the backside.

Discovery/shock model superimposed on Laherrere's graph

The big if remains whether the discovery model will correctly predict the backdated reserve growth. The equivalent URR that I fit to, 3.44 trillion barrels, reflects a value significantly higher than the 2.7 often bandied about. You can see how conservative this estimate becomes when plotted against another of Laherrere's graphs of cumulative discoveries (which has a URR of only 2.0 trillion barrels).

After doing this exercise, as you can probably tell, I've become even more of a fan of the term "undulating plateau". The cushion of potential discoveries in the future provides a modicum of slack to keep on doing what we do as consumers. Enough slack in the rope, perhaps, to hang ourselves with.

Ecotalk

AirAmerica's EcoTalk radio program may disappear soon. I listen on XM or via podcasts. Host Betsy Rosenberg apparently plowed her own money trying to keep the show alive. I had to pop some coin into the PayPal at her blog on hearing this. Of course this sickens me when you consider that CNN bankrolls cretins like Glenn Beckistan to broadcast anti-GW screeds.


Update: Richard Heinberg on Ecotalk yesterday discussing peak oil and the oil depletion protocol [MP3].

Oil of Hate

Every once in a while, the WFMU blog posts something like this catalog of songs.

S/W FI

The true measure of the cost of gas by comedy writer Chris Kelly posting at HuffPo

The Springsteen/Wilson Freedom Index
Minimum Wage (in miles)

2007 33.6 miles
2004 53.6 miles
2000 66 miles
1996 69.2 miles
1992 71.4 miles
1988 69.6 miles
1984 51.6 miles
1980 50.8 miles
1976 77.8 miles
1972 88.8 miles
1968 94 miles
1964 83.2 miles
1960 64.4 miles
1956 66.6 miles

Sources: Energy Information Administration / US Department of Labor

Your mileage may vary.

Oil for Fools

If you wander around the true-believer right-wing of the blogosphere enough, you will find that the "Oil for Food" scandal still ranks as the most favored energy topic. Rare that you will find a mention of Peak Oil, energy alternatives, or conservation, because it does not fit any of the fundamental 'minionist talking points frames, which remain that of gOD's bountiful harvest and the power of the free-market.

Well, now we see that Chevron Seen Settling Case on Iraq Oil

Chevron, the second-largest American oil company, is preparing to acknowledge that it should have known kickbacks were being paid to Saddam Hussein on oil it bought from Iraq as part of a defunct United Nations program, according to investigators.

The admission is part of a settlement being negotiated with United States prosecutors and includes fines totaling $25 million to $30 million, according to the investigators, who declined to be identified because the settlement was not yet public.

The penalty, which is still being negotiated, would be the largest so far in the United States in connection with investigations of companies involved in the oil-for-food scandal.

The $64 billion program was set up in 1996 by the Security Council to help ease the effects of United Nations sanctions on Iraqi civilians after the first gulf war. Until the American invasion in 2003, the program allowed Saddam’s government to export oil to pay for food, medicine and humanitarian goods.

Using an elaborate system of secret surcharges and extra fees, however, the Iraqi regime received at least $1.8 billion in kickbacks from companies in the program, according to an investigation completed in 2005 by Paul A. Volcker, the former chairman of the Federal Reserve.

By imposing surcharges on the sale of crude oil, the Iraqi regime skimmed about $228 million from its oil exports.

A report released in 2004 by an investigator at the Central Intelligence Agency listed five American companies that bought oil through the program: the Coastal Corporation, a subsidiary of El Paso; Chevron; Texaco; BayOil, and Mobil, now part of Exxon Mobil. The companies have denied any wrongdoing and said they were cooperating with the investigations.

As part of the deal under negotiation, Chevron, which now owns Texaco, is not expected to admit to violating the U.N. sanctions. But Chevron is expected to acknowledge that it should have been aware that illegal kickbacks were being paid to Iraq on the oil, the investigators said.

The fine is connected to the payment of about $20 million in surcharges on tens of millions of barrels of Iraqi oil bought by Chevron from 2000 to 2002, investigators said.

These payments were made by small oil traders that sold oil to Chevron. But records found by United Nations, American and Italian officials showed that they were financed by Chevron.

The negotiations, which might take several weeks to conclude, follow an agreement reached in February by El Paso, the largest operator of American natural gas pipelines, to pay the United States government $7.73 million to settle allegations that it was involved in illegal payments under the oil-for-food program.

The settlement discussions are a result of months of work by a joint task force of the United States attorneys of the Southern District of New York and the Manhattan district attorney, Robert M. Morgenthau, with help from Italian authorities. Kent Robertson, a spokesman for Chevron, said “regarding the oil-for-food program generally, Chevron purchased Iraqi crude oil principally for use in its U.S. refineries and the United Nations approved the initial sale of all cargos ultimately purchased by Chevron.”

He said Chevron has cooperated with inquiries into the program “and we will continue to do so.”

The United States attorney’s office and the office of the New York district attorney both declined to comment.

Thus far, only former United Nations officials, individual traders and relatively small oil companies have come under scrutiny in the United States.

According to the Volcker report, surcharges on Iraqi oil exports were introduced in August 2000 by the Iraqi state oil company, the State Oil Marketing Organization. At the time, Condoleezza Rice, now secretary of state, was a member of Chevron’s board and led its public policy committee, which oversaw areas of potential political concerns for the company.

Ms. Rice resigned from Chevron’s board on Jan. 16, 2001, after being named national security advisor by President Bush.

Sean McCormack, a State Department spokesman, referred inquires to Chevron.

According to Chevron’s Securities and Exchange Commission filings, the public policy committee met three times in the course of 2000. Chevron declined to comment about the private deliberations of its board.

On Jan. 26, 2001, Patricia Woertz, then president of Chevron Products, stated in an internal communication that “the payment of such a surcharge is prohibited by U.N. sanctions against Iraq,” according to documents provided by Chevron to the Volcker committee.

In any transaction involving Iraqi oil, Ms. Woertz wrote that the company should consider the “identity, experience and reputation of the selling company,” as well as “any deviation of the proposed pricing basis or margin for the transaction from historical practice.”

According to American and Italian investigators, however, a list of Iraqi oil transactions from June 2000 to December 2002, which Chevron provided to the Volcker committee, showed that the premium Chevron was paying to third parties went up after August 2000, when the illegal surcharges began — and continued to be paid even after Ms. Woertz’s warnings.

The company also did not carry out Ms. Woertz’s demand for what amounted to a credibility check on companies that sold Iraqi crude to Chevron. Chevron bought tens of millions of barrels of Iraqi oil from companies that included previously unknown players with no record in the oil business, investigators say.

One such company was Erdem Holding, which sold Chevron 13 million barrels of oil, according to Chevron’s list. This company was owned by Zeynel Abidin Erdem, a Turkish businessman who sat on the board of the Turkish-Iraqi Business Council.

On Feb. 15, 2001, about two weeks after Ms. Woertz’s internal memo was sent, Chevron bought 1.8 million barrels from Erdem, the Turkish company, at “OSP plus 36 cents.” OSP stands for the official selling price approved by the United Nations for Iraqi oil.

On other occasions, the extra payment went as high as 49.5 cents a barrel, according to the Chevron list.
...

Figures.

bin packing

Unification

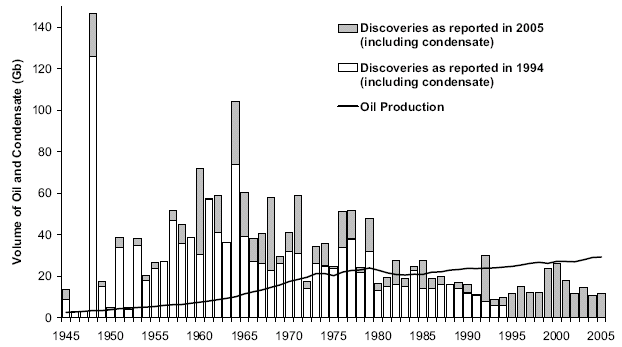
I envision the modeling of global oil depletion as the intersection of perhaps three salient behaviors: the dynamics of oil extraction, the dynamics of oil discovery, and the effects of reserve growth. I figure that I have a good handle on the first two behaviors, governed by the Oil Shock Model and the Cubic Growth Discovery Model. The mathematical convolution of the two gives, in my opinion, a great first-order view of historical oil production. However, I have not figured out exactly how to slip reserve growth into the framework to help us get some additional predictive utility out of the model. Which leads to my ongoing quest for a suitable unifying factor to bridge the three dynamics.

Khebab has done yeoman's work in trying to figure out how to retrofit a reserve growth term to the Oil Shock Model. He essentially first pointed out the (same) limited predictive utility of relying on discoveries without a reserve-like growth term serving to "soften the landing". However, I understand Khebab's modification to the OSM only up to a point. My personal impasse occurs at deciding the point in time at which we introduce reserve growth into the dynamics, and in particular whether it should occur at discovery (i.e. a form of backdating) or during the field maturation phase. Both of these stem from some basic physical considerations -- namely in the fact that it takes some mean time from the moment of discovery to the generation of a mature producing field. But that may in fact prove a bit too concrete an assumption and I have come to realize that I should rethink how discovery estimates actually figure in to the life-cycle. I have a feeling it really has to do with appearances and our perception of a discoverable quantity. After all, this perception provides the only basis for how much an oil company plans to drill in a promising region at any given moment in time.

To fuzzify the discovery term I refer back to a recent post on how reserve growth estimates on a single region may actually play out, paying careful consideration to the limits of human perception. In that micro-model, we take the simple premise that our estimate of the reserve remains proportional to the depth of knowledge of the reserve, and the variance of this estimate equaled the estimate itself (a maximum entropy estimator). I referred to this as a "depth of confidence" random variable. The fuzziness of the random variable allows it to bleed into the fixed/finite depth of the actual reservoir. So in a statistical sense, fuzzy perception mixes together an estimate that includes a concrete notion of how far we can measure into the pool (i.e. the mean) together with a fluctuating variance that could include probes beyond the fixed size of the reservoir. Although I would not go so far as to say that it follows any kind of quantum mechanical uncertainty principle, the analogy certainly applies.

I reproduce the basic estimation equations below:

The third line basically splits out the current conservative measure with a probability that we have extended beyond the depth of the finite pool. The reason for the slow uptake in reserve growth lies in the fact that as the "depth of confidence" increases, our variance also increases. So we have two competing effects: as we get closer to the fixed volume in our depth variable, the fuzziness in our estimate continues to increase, leading to a slow asymptotic glide to the final ultimate reserve limit. This essentially puts a mathematical framework on how we improve our perception of a largely unmeasurable quantity -- i.e. the fixed volume of a largely hidden reservoir buried beneath the earth. As a caveat, if you personally don't believe in the sqrt(variance) ~ mean premise, you won't get the exponential term in the preceding equation, and the reserve growth is linear until it hits the finite limit and then table-tops, i.e. no gradual asymptotic reserve growth. So in essence, we have a model that reflects perception of what we know for a discovered amount rather than the reality of the discovery -- something in fact largely unknowable or, at the very least, speculative within bounds.

The unifying connection between reserve growth on a single reservoir and estimates of discovery on a larger, or even global, scale involves only substituting a suitable expression for the "depth of confidence" growth term with time. For a single reservoir, we can assume that the depth term grows at least linearly with time, since the estimates will start improving immediately after discovery. However, for the global largely unexplored region, the equivalent depth grows geometrically over time (say like a cubic growth), as ever increasing swatches of volume are evaluated for oil content starting from the historical start of modern oil exploration in 1858.

This leads to the following equation for cumulative discovery (asymptotic value=D0):

D = kt4*(1-exp(-D0/kt4))

and the derivative of this for instantaneous discoveries (e.g. yearly discoveries):

dD/dt = 4kt3*(1-exp(-D0/kt4)*(1+D0/kt4))

We show the discovery profile for the dimension-less dD/dt below:

Note that the reserve component leaps out, as the profile has a pronounced tail. This basically provides the missing link between the previous cubic model's two physical regimes:

It took me awhile to merge the rather stark decline that occurs from hitting the discovery volume limit (which I modelled as a negative feedback term) with a gradual downslope that I figured had to occur from a diminishing return caused by the perception of apparent reserve growth.

Now I don't personally know the name of the specific mathematical formality that this model likely follows (the converse of Simulated Annealing?). I know it exists somewhere, but I don't feel bad that I don't know it at the moment. After all, the geniuses at Shell, Exxon, BP, and countless geologists haven't yet placed it either, or even stumbled across it, as far as I can tell.

As a bottom-line, I finally have my Holy Grail (I'm not dead yet) of a unified Discovery+Reserve+Shock model. This should allow some fairly robust predictive capability. Stay tuned.

Why we do the math

To irritate GlennBeckistan:

I just had a call last week, a guy says, "My son was in math, and he's watching Inconvenient Truth. What does An Inconvenient Truth have to do with math?"