Tower of Babel, How languages diversify

One pattern that has evaded linguists and cognitive scientists for some time relates to the quantitative distribution in human language diversity. Much like how plant and animal species diversify in a specific pattern, with very few species dominating within an ecosystem and relatively few species exceedingly rare, the same thing happens with natural languages. You find a few languages spoken by many people, and very few spoken seldomly,with the largest number occupying the middle.

Consider a simple model of language growth whereby adoption of languages occur over time by dispersion. The cumulative probability distribution for the number of languages is

P(n) = 1/(1+1/g(n))

This form derives from the application of the maximum entropy principle to any random variate where one only knows the mean in the growth rate and an assumed mean in the saturation level. I refer to this as entropic dispersion and have used this many applications before so I no longer feel a need to rederive this term every time I bring it up.

The key to applying entropic dispersion is in understanding the growth term g(n). In many cases n will grow linearly with time so the result will assume a hyperbolic shape. In another case, an exponential growth brought up by technology advances will result in a logistic sigmoid distribution. Neither of these likely explains the language adoption growth curve.

Intuitively one imagines that language adoption occurs in fits and starts. Initially a small group of people (at least two for arguments sake) have to convince other people on the utility of the language. But a natural fluctuation arises with small numbers as key proponents of the language will leave the picture and the growth of the language will only sustain itself when enough adopters come along and the law of large numbers starts to take hold. A real driving force to adoption doesn't exist, as ordinary people have no real clue as to what constitutes a "good" language, so that this random walk or Brownian motion has to play an important role in the early stages of adoption.

So with that as a premise, we have to determine how to model this effect mathematically. Incrementally we wish to show that the growth term gets suppressed by the potential for fluctuation in the early number of adopters. A weaker steady growth term will take over once a sufficiently large crowd joins the bandwagon.

dn = dt / (C/sqrt(n) + K)

In this differential formulation, you can see how the fluctuation term which goes as 1/sqrt(n) suppresses the initial growth until it reaches a steady state as the K term becomes more important. Integrating this term once and we get the implicit equation:

2*C*sqrt(n) + K*n = t

Plotting this for C=0.007 and K=0.000004, we get the following growth function.

Figure 1 : Growth function assuming suppression during early fluctuations

This makes a lot of sense as you can see that growth occurs very slowly until an accumulated time at which the linear term takes over. That becomes the saturation level for an expanding population base as the language has taken root.

To put this in stochastic terms assuming that the actual growth terms disperse across boundaries, we get the following cumulative dispersion (plugging the last equation into the first equation to simulate an ergodic steady state):

P(n) = 1/(1+1/g(n)) = 1/(1+1/(2*C*sqrt(n) + K*n))

I took two sets of the distribution of population sizes of languages (DPL) of the Earth’s actually spoken languages from the references below and plotted the entropic dispersion alongside the data. The first reference provides the DPL in terms of a probability density function (i.e. the first derivative of P(n)) and the second as a cumulative distribution function. The values for C and K were as used above. The fit works parsimoniously well and it makes much more sense than the complicated explanations offered up previously for language distribution.

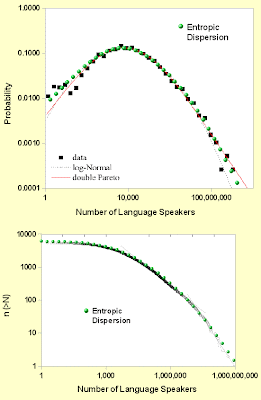Figure 2 : Language diversity (top) probability density function (below) cumulative. The entropic dispersion model in green.

In summary, the two pieces to the puzzle are assuming dispersion according to the maximum entropy principle, and a suppressed growth rate due to fluctuations during the early adoption. This gives two power law slopes in the cumulative; 1/2 in the lower part of the curve and 1 in the higher part of the curve.

References

1. Scaling Relations for Diversity of Languages (2008)
2. Competition and fragmentation: a simple model generating
   lognormal-like distributions (2009)
3. Scaling laws of human interaction activity (2009)
   Discussions on the fluctuation term.
   

---

NY Math Teacher Howard A. Stern Uses Ingenuity To Overcome Failure Statistics

The public school teacher highlighted in the linked article has this to say:

"So much of math is about noticing patterns," says Stern, who should know. Before becoming a teacher, he was a finance analyst and a quality engineer.

I always try to seek interesting patterns in the data, but more to the point, I try to actually understand the behavior from a fundamental perspective.

One way Stern uses technology is by helping his students visualize his lessons through the use of graphing calculators.

Stern has it exactly right, if we treat knowledge seeking as a game, like a suduko puzzle, we can attract more people to science in general.

I think that the pattern in language distribution has similarities to that of innovation adoption as well, similar to what Rogers describes in his book "Diffusions of Innovations". I will try to look into this further as I think the dispersive arguments holds some promise as an analytical approach.

---