Hubbert peak in Five Easy Pieces
Based on the increase in spill rate from the leaking Gulf of Mexico oil well, HO at TheOilDrum.com suggested a potential explanation. His post essentially argued that sand particles acting as a strong abrasive driven along by the already high velocity stream of escaping oil leads to increasing in the channeling and thus an even faster leak rate.
HO described a process known as CHOPS (Cold Heavy Oil Production with Sand) which can enlarge a well's streaming throughput by promoting the formation of heavily eroded channels. The TOD post provided the following picture of the possible outcome of the behavior.
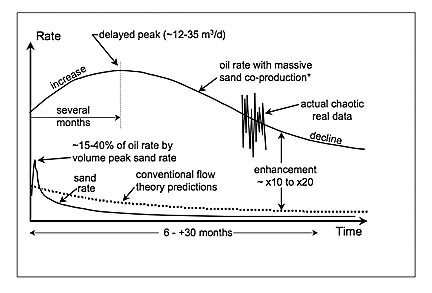 Note that the lower curve shows the typical output from a throttled flow. Above that curve, the modulated line shows the results of an accelerated extraction -- note that a peak actually appears which pinpoints the maximum flow rate. In terms of the oil spill, we don't want this behavior because it gives us less time to fix or relieve the problem well. Yet, ordinarily we want this same behavior -- that of fast extraction -- in practical situations because we want and need the oil right now! (so that oil companies can make money, of course)
Note that the lower curve shows the typical output from a throttled flow. Above that curve, the modulated line shows the results of an accelerated extraction -- note that a peak actually appears which pinpoints the maximum flow rate. In terms of the oil spill, we don't want this behavior because it gives us less time to fix or relieve the problem well. Yet, ordinarily we want this same behavior -- that of fast extraction -- in practical situations because we want and need the oil right now! (so that oil companies can make money, of course)Which leads me to formulating the following very simple but physically correct model of Hubbert's Peak. You won't find this anywhere else, because this derivation does not jive with how geologists think about oil extraction. They get many of the pieces but they never put them all together.
I will offer up a derivation for this behavior leading to a Hubbert Peak in 5 easy pieces.
Piece 1. The standard assumption of draw-down from a reservoir results in an exponential decline over time. You can consider that the exponential shape results from a law of diminishing returns; in that a constant amount proportional to the remainder draws down per unit time. Or you can say that a maximum entropy range of extraction rates gets applied to the volume. A proportional extraction rate that we call R defines the mean and U0 is the reservoir size. U(t) gives us the cumulative reserve.
U(t) = U0*exp(-R*t)
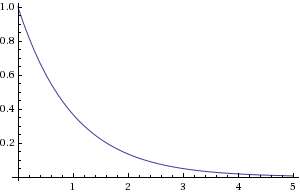
Piece 2. Next, we realize that we have uncertainty over the size of the reservoir; the U0 we have defined actually only serves as an estimate of the size. This means we have an uncertainty over the rate of proportional extraction as well. This turns into a form of hyperbolic discounting and the cumulative draw-down actually looks like this.
U(t) = U0 / (1+R*t)

Piece 3. Next we assert that the constant but uncertain proportional extraction rate undergoes an acceleration starting from the original value, R(t) = R0 + k*t. This acceleration equates to Newton's law, first-order with time. Then the instantaneous absolute rate of extraction from the remaining reservoir looks like:
RateOfExtraction(t) = -dU(t)/dt = U0*(R0 + k*t)/(1+R0*t+k*t2/2)2For R0=0.5 and k=2, it results in this shape
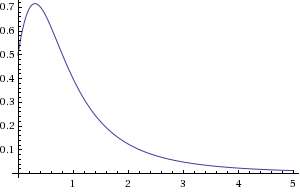
This curve we can scale and overlay on top of the CHOPS curve to validate our thought process.

Piece 4. Over a larger set of reservoirs that experience a technical improvement over time, we can assume that the proportional extraction rate can accelerate even more strongly over time, R(t)=C*exp(k*t). This gives us a Moore's law form of acceleration, doubling every set number of years. Then
RateOfExtraction(t) = -dU(t)/dt = U0 * R(t) / (1+integral(R(t)dt))2For a small starting rate, the acceleration further accentuates the subtle peak that we observe in piece 3 and it turns into a full-fledged symmetric peak as shown in the next figure:
= U0*C*exp(k*t)/(1+C/k*(exp(k*t)-1))2

Piece 5. Congratulations. You haven't broken any rules and you have just derived the famed Hubbert Peak, also known as the Logistic Sigmoid function.
Some Backstory
An alternate derivation exists for the corresponding discovery peak, which I call Dispersive Discovery. There, the uncertainty involves how much volume gets explored and at what rate, otherwise the math turns out exactly the same. Both derivations result from an assumed finite constraint but uncertainty in both rates and subvolumes. The only problem with using the Hubbert peak derivation for extraction is that it premises that each extraction rate started at the same time (globally this would be 1858). We know that this has not happened for global production, as extraction can only start after a discovery, and then some variable hold time. By using dispersive discovery, we get a larger spread in start years, and then The Oil Shock model generates the extraction curve. In general, if the discovery peak precedes the oil production peak by a number of years, I would use Dispersive Discovery, but if the two coincide, then extraction tracks discovery and it doesn't really matter how you interpret the rates. This explains why this particular derivation works well for more localized production areas that have seen significant technology changes. In contrast, the technology of discovery has undergone tremendous technology changes over the years, so that dispersive discovery works very well in terms of global modeling. This is actually not much of a caveat, as the more ways that you can find the same result, the more confidence you have that you have remained on the right track.
The current derivation also points out the huge hole in the technique known as Hubbert Linearization (HL). As defined, HL derives from the observation that
dU(t)/dt = U(t)*(U0-U(t))Yet this only works for the one case where we can define R(t) as an exponential function, that of piece 4. The formula does not work for either piece 1, 2, or 3. Therefore, HL only serves as a curious mathematical identity for that one exponential case, which we know does not always occur.
The actual "WebHub" Linearization takes the following form:
dU(t)/dt = -U0 * R(t) / (1+integral(R(t)dt))2This may not prove as handy as HL perhaps, but it has the benefit of correctness, and it works well for certain cases.
Like me, Robert Rapier has railed against the inadequacy of HL and this may take up the slack.









0 Comments:
Post a Comment
<< Home