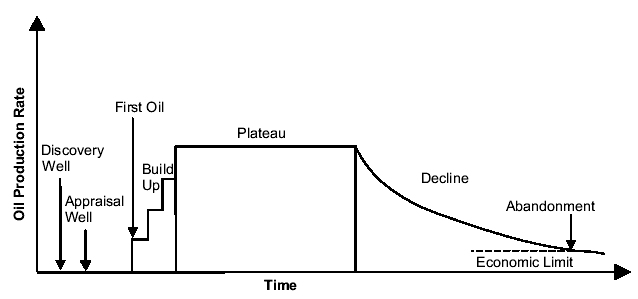
Shocklets
The Oil Shock Model uses a simple rather unbiased multiplier to estimate the oil production response to a discovery input. To demonstrate this, let us take a particular sub-case of the model. If we assume that a discovery immediately becomes extractable, then the multiplying factor for instantaneous production becomes a percentage of what remains. This turns into a damped exponential for a delta discovery (delta meaning a discovery made at a single point in time). In practice, this means that for any particular discovery in the Oil Shock model, we immediately enter a regime of diminishing returns. You can see this in the following plot.

One could argue pragmatically that we rarely enter into an immediately diminishing return regime. In fact, we have all seen the classical regime of an oil bearing region --- this often features an early constant plateau, followed by a drop-off after several years. We usually take this to mean that the oil producers deliberately decide to maintain a constant production rate until the wells no longer produce, in which case we then enter the damped downslope. Or else this could imply that the oil pressure maintains a certain level and the producers extract at the naturally established equilibrium. In fact, the reason that I chose the damped exponential for the Oil Shock model has nothing to do with the intricacies of production; instead it really has to do with the statistics of a spread or range of oil producing wells and regions. The unbiased multiplier really comes from the fact that bigger oil discoveries produce proportionately more oil than smaller oil discoveries, which naturally have less oil to offer. This model becomes nothing more or less than an unbiased statistical estimator for a collection of oil-bearing regions. In other words, the statistics of the collective reduces to a single instance of an average well if we want to think it through from a macro to a micro-perspective. So as a large discovered region starts to deplete, it tends to look statistically more and more like a small producing region, and therefore the fractional extraction estimator kicks in.
With all that said, I can come up with a simple discovery model that matches the behavior of the early plateau observations. We still assume the fractional extraction estimator, but we add in the important factor of reserve growth. Consider the following figure, which features an initial delta discovery at year 1, followed by a series of reserve growth additions of 10% of the initial value over the next 10 years. After that point the reserve growth additions essentially drop to zero.

Next consider that the the extraction essentially scales to the amount of reserve available, and so we set the extraction rate arbitrarily to 10% of the remaining reserve, calculated yearly. (The choice of 10% is critical if you do the math, explained below [1]) Therefore, for a discovery profile that looks like an initial delta function followed by a fixed duration reserve growth period, for the appropriate extraction rate we can come up with the classical micro-production profile.

Wonder of wonders, we see that this micro-model approximates the classical observation of the early plateau followed by a damped exponential. Not coincidentally, the plateau lasts for the same 10 years that the reserve growth takes place in. Rather obviously, we can intuit that this particular plateau maintains itself solely by reserve growth additions. So as the diminishing returns kick in from the initial delta, the reserve growth additions continuously compensate for this loss of production level, as long as the reserve growth maintains itself. After this, the diminishing returns factor eats at whatever reserves we have left, with no additional reserve growth to compensate for it. Voila, and we have a practical model of the classical regime based on the Oil Shock model.
The troublesome feature of the classic plateau lies in its artifice. The underlying discovery model consists of sharp breaks in the form of discontinuities. These manifest themselves in discontinuities in the production model. You see that in the kick-start to immediate stable production due to a delta function in discovery, and then a sharp change in slope due to the sudden end of reserve growth. I don't think anyone actually believes this and I know that Khebab has the same view as he previews in a comment on TOD:
So from this figure and discussion, we know we must at least account for the build-up, or what I would call the Maturation phase in the Oil Shock model. (The Oil Shock model also considers the Discovery phase and Construction phase but we can ignore these for the purposes of this discussion) This next figure from Khebab aggregates a bunch of these plateau-shaped production profiles from the UK and Norway (where the individual governments' requires close accounting of production levels from the field owners) :"Now, if you have additional information (peak date, plateau duration, URR, etc.), you could use a more complex model such as the one used by Robelius in his PhD thesis:
I'm currently working on a more complex model."
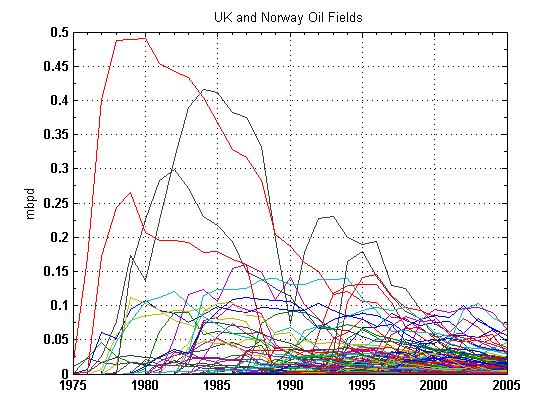 Even though the figure looks busy, note that almost all the profiles show the build-up phase fairly clearly. You can also observe that very few show a stable plateau, instead they mostly show a rounded peak followed by a decline. The asymmetry shows longer tails in the decline than the upward ramp during the build-up phase.
Even though the figure looks busy, note that almost all the profiles show the build-up phase fairly clearly. You can also observe that very few show a stable plateau, instead they mostly show a rounded peak followed by a decline. The asymmetry shows longer tails in the decline than the upward ramp during the build-up phase. I contend that the Dispersive Discovery model of reserve growth entered into the Oil Shock model can handily generate these kinds of profiles.
The Idea of Shocklets
Khebab has investigated the idea of using loglets (similar to wavelets) in understanding and fitting to multiple-peak oil production profiles. He also used characteristics of the loglet to construct the HSM (and I safely assume his more complex model he hinted at above). As the basic premise behind these "X-let" transforms you find a set of sample signals that when scaled and shifted provides a match to the profile of, say, an oil production curve under examination or some other temporal wave-form. The Oil Shock Model does not differ much in this regard; this salient connection just gets buried in the details of the math [2].So I suggest that we can visualize the characteristic oil shock model profile by constructing a set of "shocklets" based on the response from a discovery profile input stimulus. The shocklets themselves become micro-economic analogies to the macro view. The math essentially remains the same -- we just use a different prism to view the underlying mechanism.
At the beginning of this discussion, we essentially verified the premise of shocklets by mimicing the plateau regime via a simple discovery/reserve/extraction shock model. That gave us the classical "flat-topped" or plateaued production profile. To modulate the discontinuities and flatness, we use the technique of convolution to combine the damped exponential extraction phase with a modeled maturation phase. The basic oil shock model proposed a simple maturation model that featured a damped exponential density of times; this described the situation of frequent fast maturities with a tail distribution of slower times over a range of production regions.
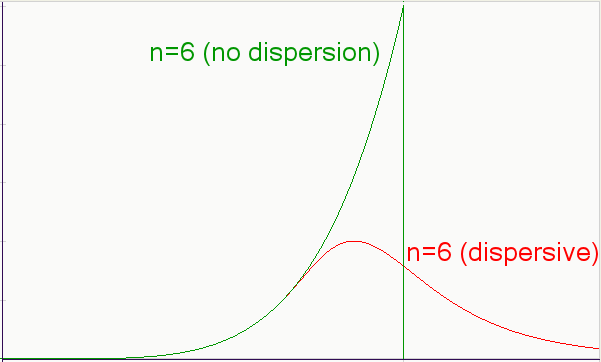
The exponential with exponential convolution gives the following "shocklet" (with both maturation and extraction characteristic times set to 10 years). Note the build-up phase generated by the maturation element of the model, with very little indication of an extended plateau. (Bentley has a recent TOD post up where he draws a heuristic with a similar shape without providing a basis for its formulation, see the figure to the right)

Now, with a recently established reserve growth model, we can replace the maturation curve with the empirically established reserve growth curve. I make the equivalence between a maturation process and reserve growth additions simply because I contend that extraction decisions get based primarily by how how much reserve the oil producers think lies under the ground -- other maturation effects we can estimate as second-order effects. This essentially makes the connection to and unifies with Khebab's deconvolution approach from backdated discoveries, where he applies Arrington's reserve growth heuristic to the oil shock model and its hybrid HSM. The key idea from Khebab remains the use of the best reserve growth model that we have available, because this provides the most accurate extrapolation for future production.
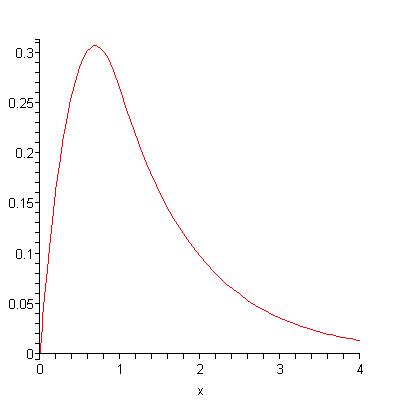
We start with a general reserve growth curve L2/(L+Time)2 derived from the Dispersive Discovery model. The following figure looks a lot like an exponential (the characteristic time for this is also 10 years) but the DD reserve growth has a sharper initial peak and a thicker longer tail. Compare this to the artificially finite reserve growth profile used to generate the idealized plateau production profile at the beginning of this post.

The shocklet for the DD reserve growth model looks like the following profile in the figure below. Note the build-up time roughly equates with the exponential maturation version, but the realistic reserve growth model gives a much thicker tail. This matches expectations for oil production in places such as the USA lower-48 where regions have longer lifetimes, at least partially explained by the "enigmatic" reserve growth empirically observed through the years. The lack of a long flat plateau essentially occurs due to the dynamics of reserve growth; nature rarely compensates a diminishing return with a precisely balanced and equivalent reserve growth addition. And this matches many of the empirically observed production profiles. The perfectly flat plateau does exist in the real world but the frequent observation of a reserve growth shocklet shape makes it much more useful for general modeling and simulation (the two parameters for characterizing the shape, i.e. an extraction rate and a reserve growth time constant, makes it ultimately very simple and compact as well).

The mantra of the Oil Shock Model still holds -- every year we always extract a fraction of what we think lies underground. The role of reserve growth acts to provide a long-term incentive to keep pumping the oil out of certain regions. As the estimates for additional reserve keep creeping up over time, a fraction of the oil consistently remains available. And by introducing the concept of shocklets, we essentially provide a different perspective on the utility of the Oil Shock Model.
[1] The solution to the delta plus finite constant reserve shock model is this set of equations:
| Po(t) = k e-kt | -- production from initial delta, for all t |
| P1(t) = C (1 - e-kt) | -- production from reserve, for t <> |
| P2(t) = C e-kt (ekT - 1) | -- production from reserve, for t > T |
[2] Shifting, scaling, and then accumulating many of these sampled waveforms in certain cases emulates the concept of convolution against an input stimulus. For a discovery stimulus, this relates directly to the Oil Shock Model.