Macro Peak Oil Model vs Logistics Curve

Stuart Staniford posting at The Oil Drum tried out some fits of a logistics curve to oil production data from Beyond Petroleum/British Petroleum's report on World Energy 2005. He noted:

In the beginning, the data are crazy, but after about 1958, they settle down into pretty much a linear regime (with a little noise) that has held good ever since. The nice thing about this method is that you do not need to input an estimate for the URR. Instead, you extrapolate the straight line, and it tells you the URR.

I find the highlighted part revealing in that Staniford conveniently sweeps perfectly good data under the rug. I always say never attribute to crazy what probably has a rational explanation.

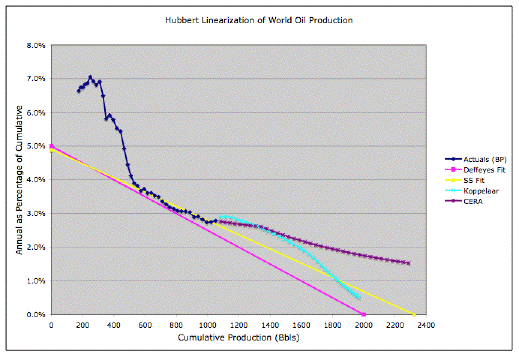
So what exactly causes that initial precipitous drop in the dark blue curve that nobody wants to fit to? And why do analysts want to work in the so-called "stable" regime where the logistics curve seems to work so well? Well, I believe it has to do with the use of the logistics curve itself, which has no intuitive meaning to how the world actually works.

I came up with a more realistic yet very simple depletion model a few months ago in two posts called A Macro Peak Oil Model, Part 1 and Part 2. You can review the details at the two links, but a typical model result looks like the following yellow "Bell-shaped" curve:

To match up against the logistics curve plot, which Staniford and Deffeyes use to "linearize" the data,

dQ/dt / Q = k(1-Q)

I simply had to integrate the simple production curves to obtain the cumulative (Q) number. My plot looks like the following, with a depletion rate of 0.03/year tacked on to the 130-year-span triangular discovery curve:

Notice that we get a perfectly understood dropoff (perhaps quasi-hyperbolic) before it settles into a more-or-less linear regime as at heads to a zero production rate when we hit the cumulative production limit.

I will look into the details a bit more later, but for now it appears a bit more optimistic than the logistics fit, as it tends to flatten out in the out years.