Double Dispersive Discovery leads to the Sigmoid and Logistic

I believe I made a significant finding in regards to the Dispersive Discovery model. In its general form, keeping search growth constant, the dispersive part of the model produces a cumulative function that looks like this:

D(x) = x * (1-exp(-k/x))

The instantaneous curve generated by the derivative looks like

dD(x)/dx = c * (1-exp(-k/x)*(1+k/x))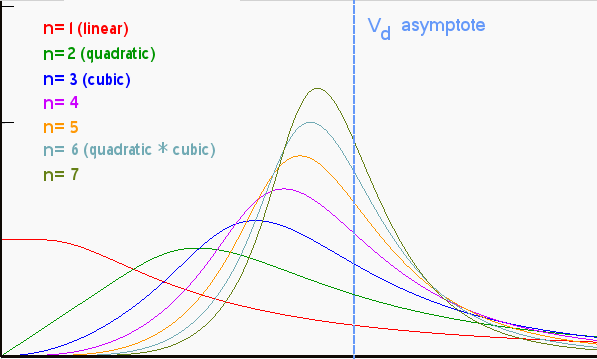

Adding a growth term for x and we can get a family of curves for the derivative:

I generated this set of curves simply by applying growth terms of various powers, such as quadratic, cubic, etc, to replace x. No bones about it, I could have just as easily applied a positive exponential growth term here, and the characteristic peaked curve would result, with the strength of the peak directly related to the acceleration of the exponential growth. I noted that in an earlier post:

As for as other criticisms, I suppose one could question the actual relevance of a power-law growth as a driving function. In fact the formulation described here supports other growth laws, including monotonically increasing exponential growth.

Overall, the curves have some similarity to the Logistic sigmoid curve and its derivative, traditionally used to model the Hubbert peak. Yet it doesn't match the sigmoid because the equations obviously don't match -- not surprising since my model differs in its details from the Logistic heuristics.

However, and it starts to get really interesting now, I can add another level of dispersion to my model and see what happens to the result. I originally intended for the dispersion to only apply to the variable search rates occurring over different geographic areas of the world. But I hinted that we could extend it to other stochastic variables:

We have much greater uncertainties in the stochastic variables in the oil discovery problem, ranging from the uncertainty in the spread of search volumes to the spread in the amount of people/corporations involved in the search itself.

So I started with a spread in search rates given as an uncertainty in the searched volume swept, and locked down the total volume as the constant k=L0. Look at the following figure, which show several parts of the integration, and you can see that the uncertainties only reflect in the growth rates and not in the sub-volumes, which shows up as a clamped-asymptote below the cumulative asymptote:

I figured that adding uncertainty to this term would make the result more messy than I would like to see at this expository level. But in retrospect, I should have taken the extra step as it does give a very surprising result.

That extra step involves a simple integration of the constant k=L0 term as a stochastic variable over a damped exponential probability density function (PDF) given by p(L)=exp(-L/L0)/L0. This adds stochastic uncertainty to the total volume searched, or more precisely, uncertainty to the fixed sub-volumes searched, that when aggregated provide the total voluume.

D(x) = Integral [ x * (1-exp(-L/x))*exp(-L/L0)/L0 dL ]

This turns into a trivial analytical integration from L=0 to L=infinity. The result becomes the simple relation:

D(x) = 1/(1/L0 + 1/x)

Note that the exponential term from the original dispersive discovery function disappears. This occurs because of dimensional analysis: the dispersed rate stochastic variable in the denominator has an exponential PDF and the dispersed volume in the numerator has an exponential PDF; these essentially cancel each other after each gets integrated over the stochastic range.

In any case, the simple relationship that this gives, when inserted with an exponential growth term such as A*e^B*t, results in the logistic sigmoid function:

D(t) = 1 / (1/L₀ + 1/(A*e^B*t))

I will make the next statement in as passive a voice as possible. This is the Holy Grail derivation of the Logistic curve.

Seriously, I don't think anyone has ever figured out how to derive the Logistic in such fundamental terms until now. The logistic has now transformed from a cheap heuristic into a model result. The fact that it builds on the Dispersive Discovery model gives us a deeper understanding of its origins. So whenever we see the logistic sigmoid used in a fit of the Hubbert curve we know that several preconditional premises must exist:

1. It models a discovery profile.
2. The search rates are dispersed via an exponential PDF
3. The searched volume is dispersed via an exponential PDF
4. The growth rate follows a positive exponential.

This finding now precludes other meaningless explanations for the Logistic curve's origin, including birth-death models, predator-prey models, and other ad-hoc carrying capacity derivations that other fields of scientific study have traditionally incorporated into their temporal dynamics theory. None of that matters, as the Logistic -- in terms of oil discovery -- simply models the stochastic effects of randomly searching an uncertain volume given an exponentially increasing average search rate. In the end, intuition has always told me this, and the math has served as a formal verification of my understanding. You have to shoot holes in the probability theory to counter the argument, which any good debunking needs to do.

As a very intriguing corollary to this finding, the fact that we can use a Logistic to model discovery means that we cannot use a Logistic to model production. I have no qualms with this turn of events as production comes about as a result of applying the Oil Shock model to discoveries, and this essentially shifts the discovery curve to the right in the timeline while maintaining most of its basic shape. (And as another bit of insight, consider the application of multiple Logistic curves to model complicated scenarios. The fact that I just integrated multiple stochastic volumes over a search space to derive the logistic raises questions about the validity of such an approach. This really needs a fundamental analysis as it would necessarily duplicate the integration I have already accomplished. Unfortunately, such misuse happens when a curve gets used as a heuristic, separated from its first principles derivation.)

In spite of such a surprising revelation, we can continue to use the Dispersive Discovery in its more general form to understand a variety of parametric models, which means that we should remember that the Logistic manifests itself from a specific instantiation of dispersive discovery. Good to have this chapter closed, as the origin of the Logistic had become a nagging obsession of mine over the past few years. I can basically put it to rest, which will maintain my sanity for awhile.

---

As a corollary, given the result:

D(x) = 1/(1/L0 + 1/x)

we can verify another type of Hubbert Linearization. Consider that the parameter x describes a constant growth situation. If we can plot cumulative discovered volume (D) against cumulative discoveries or depth (x), we should confirm the creaming curve heuristic. In other words, the factor L should remain invariant allowing us to linear regress a good estimate of ultimate volume :

L0 = 1/(1/D - 1/x)


It looks like this might arguably fit some curves better than previously shown.