Gold Rush dynamics, the Dispersive Discovery sanity check

Dynamics such as those that lead to extinction events and of boom-bust periods first motivated me to generalize discovery dynamics in terms of dispersive effects.

If we look into an extinction event such as passenger pigeons in the 1800's, we find a steadily accelerating harvest per year until culling hit a critical point and then fell precipitously. The harvests went spectacularly to zero and so, unfortunately, did the pigeon population.

I can say the same for boom-bust cycles, such as happened during the gold-rush days of the 1800's. In most cases, a boom occurred on the onset of an isolated discovery as many prospectors joined the search, enough time passed to enable the building of a huge infrastructure and then suddenly everything dried up with the infrastructure left standing in place.

But that hasn't happened with the discoveries of fossil fuel around the world. Although discoveries did increase at an accelerating pace until about the mid-part of the 20^the century, reaching a peak a little after 1960, many discoveries continue to occur and the bottom did not fall out, unlike the cases of extinction and nini-boom-busts. We explain this by considering the role of dispersion in the discoveries. The following figure shows a non-dispersed discovery function, which reaches a sharp peak and then drops to zero as prospectors finish searching an isolated volume of potential finds.



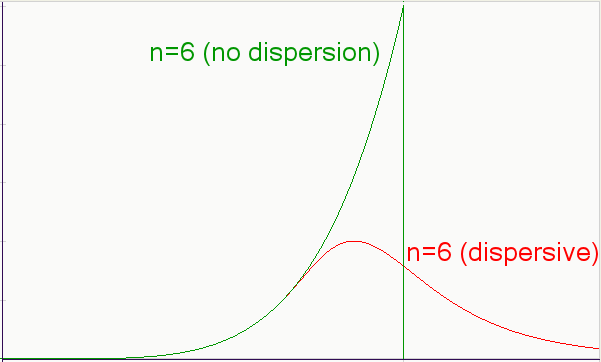
This basically happens when a highly localized search takes place, as with the case of the blanket coverage of passenger pigeon flyways with an efficient army of hunters (often equipped with explosives!). Its also happens with prospectors sifting everything with the equivalent of a fine-tooth comb in some localized gold strike area.

But the discovery of oil differs as dispersion in the rates of discovery in various parts of the world lead to a broad smearing of the bust peak. In fact, the effective bust peak (equal integrated volume) only lines up on the backside of the dispersed profile. This all makes consistent sense and provides a further argument against the use of the Logistic function to model any of these kinds of search processes, dispersed or not.

In other words someone has to explain why a symmetric Logistic function (ala the classic Hubbert curve) does not explain the steep drop-off displayed in many culling-forced extinction examples and of the bust drop-off in gold-rush cases.

Of course, this all gets the hand-wave treatment by the classically trained Hubbert modelers that use the Logistic function. Which I find really and truly odd as the Verhulst birth-death equations theoretically apply most effectively in localized Petri dish style experiments. Translation: analysis by Logistic approaches does not meet yet another sanity check and only serves as a cheap heuristic.