Popcorn Popping as Discovery

In the search for the perfect analogy to oil depletion that might exist in our experiential world, I came across a most mundane yet practical example that I have encountered so far. Prompted by a comment by Memmel at TOD who bandied about the term "simulated annealing" in trying to explain the oil discovery process, I began pondering a bit. At the time, I was microwaving some popcorn and it struck me that the dynamics of the popping in some sense captured the idea of simulated annealing, as well as mimiced the envelope of peak oil itself.

So I suggested as a reply to Memmel's comment that we should take a look at popcorn popping dynamics. The fundamental question is : Why don't all the kernels pop at the same time?

It took me awhile to lay out the groundwork, but I eventually came out with a workable model, the complexity of which mainly involved the reaction kinetics. Unsurprisingly, the probability and statistics cranked out straightforwardly as it parallels the notion of dispersion that I have worked in terms of the Dispersive Discovery Model. First, we define the basic premise with the aid of Figure 1

Figure 1: Popcorn popping kinetics. Each bin has a width of 10 seconds, and the first kernel popped at 96 seconds. So the overall width is quite large in comparison to the first pop time. Graph taken from Statistics with Popcorn [1]. The curve itself looks similar to a oil discovery peak.

In obvious ways, the envelope makes sense as experience and intuition tells us that a maximum popping rate exists which corresponds to the period of the loudest and densest popping noise. Certainly, if you stuck a thermometer in the popcorn medium you would find the average temperature rising fairly uniformly until it reaches some critical temperature. Naively, you could them imagine everything popping at once or within a few seconds of one another -- after all, water in a pop seems to boil quite suddenly. But from the figure above, the spread seems fairly wide for popcorn. The key to the range of popping times lies in the dispersive characteristics of the popcorn. This dispersion essentially shows up because of the non-uniformity among the individual kernels. Intuitively this may get reflected as variations in the activation barrier of the kernels or in the micro-variability in the medium.

Some may suggest that the temperature spread may occur simply because of the effects of the aggregation of the popcorn kernels interacting with each other as they pop. For example, one kernel popping may jostle the environment enough to effectively cool down the surrounding medium, thus delaying the effects of the next kernel. However, that remains a rather insignificant effect. I thought about doing the experiment myself until I ran across an impressively complete study executed by a team of food scientists. Measured painstakingly against temperature, the cereal scientists placed individual kernels in a uniformly heated pot of oil, and tabulated each kernel's popping time. They then plotted the cumulative times and determined the rate constants, trying to make sense of the behavior themselves (curiously, this experiment was only completed for the first time 4 years ago).

Kinetics of Popping of Popcorn, J. E. Byrd and M. J. Perona (PDF)

Anyone who has made popcorn knows that in a given sample of kernels, the kernels fortunately do not all pop at the same time. The kernels seemingly pop at random and exhibit a range of popping times (Roshdy et al 1984; Schwartzberg 1992; Shimoni et al 2001). The model described above does not explain this observation. It explains why popcorn pops, but has nothing to say about when a kernel will pop. The goal of this work was to use the methods of chemical kinetics to explain this observation. More specifically, we performed experiments in which the number of unpopped kernels in a sample was measured as a function of time at a constant bath temperature. This type of experiment has not been reported in the literature, and the data are amendable to the methods of chemical kinetics. In addition, we formulated a quantitative kinetic model for the popping of popcorn and have used it to interpret our results. The literature contains no kinetic model for the popping of popcorn.

If you read the article you note that the idea of a rate constant comes into play. In fact, you can think of the individual kernels obeying the laws of physics as they plot their own trajectory until they reach a critical internal pressure and ultimately pop. In other words, they pop at a rate that does not depend on their neighbors (since they have no neighbors in the experiment). I suggest that two mechanisms come into play with respect to the internal dynamics of the popcorn kernel. First, we have the mechanism of the starchy internal kernel which heats up at a certain rate and starts to build up in pressure over time. This happens at an average rate but with an unknown variance; let us say that has a maximum entropy such that the standard variance equals the mean, see the maximum entropy principle. Second, we have the average rate itself accelerating over time, so that the pressure both builds up and breaks down the underlying medium at a faster and faster pace. Finally, we have variations in the kernel shell (i.e. the thickness of the pericarp layer) which acts as an activation barrier, thus defining the effective exit criteria for the kernel to pop. However, this latter mechanism does not exhibit as large of a variance, as that would trigger more immediate popping and not as explosive an effect [2]. The overall process has analogies to the field of study known as "physics of failure"; each popcorn kernel eventually fails to maintain its rigidity as it pops, and just like real failure data, this is dispersed over time. Physics of failure relies on understanding the physical processes of stress, strength and failure at a very detailed level, and I apply this at a level appropriate for understanding popcorn.

Given this premise, the math works out exactly to the approach formulated for Dispersive Discovery. I use the generalized version which applies the Laplace transform technique to generate a cumulative envelope of the fraction of unpopped popcorn over time=t and oil temperature=T.

P(t,T) = 1 - exp(-B/f(t,T))/(1+A/f(t,T))

the term f(t,T) represents the mean value of the accelerating function, and the terms A and B reflect the amount of dispersion in the shell characteristics; if B=1 and A=0 the shell has a fixed breakthrough point and if B=0 and A=1 the shell has an exponentially damped breakthrough point (i.e. lots of weaker kernels) . The latter set defines the complement of the logistic sigmoid, if f(t,T) accelerates exponentially.

f(t,T) = exp(R(T,t)) - exp(R(T,0))
R(t,T) = k*(T-T_c)²*t - c*(T-_Tc)

The basic physics of failure is encompassed in the exponential term f(t,T) which states that the likelihood of failing increases exponentially over time, as the internal structure of the popcorn starts to compound its failure mechanisms. At T=T_c and below that temperature nothing ever pops. At higher temperatures than the critical temperature, the rate correspondingly increases according to a power law (see right). Temperature as related by the parameter k is the dial of the accelerator. The parameter c acts as the delay time for how long it takes the kernel to reach the equilibrium temperature of the oil.

The set of data from the Byrd and Perona experiment is shown below, along with my temperature dependent dispersive model shown as the colored lines for A=0.5, B=0.5, c=0.1/degree, T_c=170 degrees, and k=0.00008/degree²/second. The solid lines black lines are the fit to their model which essentially adjusts each parameter for each temperature set. I left the model minimally parametric over the temperature range and adjusted only the oil temperature for each curve -- in other words, they all share the base parameters.

Figure 2: Measurements of the fraction of unpopped popcorn remaining as a function of time over a range in oil cooking temperatures (in degrees C). Two timescales are shown. These can be compared to the complementary sigmoid functions.

The authors of the study don't use the same formulation as I do because the theorists don't tend to apply the fat-tail dispersion math that I do. Therefore they resort to a first-order approximation which uses a Gaussian envelope to generate some randomness. They essentially do the equivalent of setting the B term to 1 and the A term to 0. This really shows up in the better fit at low temperatures at early popping times -- see the green curve at T=181.5 degrees in Figure 2 which tends to flatten out at earlier times than their model. Overall the fit is extremely good over the range of curves, as I contend that any deviations occur because of the limited sample size of the experiments. It gets awfully tedious to measure individual popping times and the fluctuations from the curve will surely arise. You can see this in a magnification of the low-temperature data set shown to the right. If you notice some of the 200 degree data points pop later than the 190 degree data points. These occur solely due to statistical probability artifacts due to the small sample size (between 50 and 100 kernels per experiment at the temperature measured). If they had at least 500 measurements per data set the fluctuations would have decreased by at least a factor of two. You can also observe that the statistical fluctuations show up very well if plotted as a frequency histogram in Figure 3 below. Compare this set against Figure 1, which smooths out the curve via larger bins.

Figure 3: The set of "Hubbert Curves" for popping popcorn at several temperatures.

Each one of the curves gets transformed into something approaching a logistic curve as the temperature accelerates in temperature and then keeps rising. You can think of the individual pops as those kernels meeting the criteria for activation. The laggards include those kernels that haven't caught up, either intrinsically or because of the non-uniformity of the medium (as a counter-example, water is uniform and it mixes well).

The upshot is that this popcorn popping experiment stands as an excellent mathematical analogy for dispersive discovery. If we consider the initial pops that we hear as the initial stirrings of discrete discoveries, then the analogy holds as the popping builds to a crescendo of indistinguishable pops as we reach peak. After that the occasional pop makes its way out. This happens with oil discovery as well, as the occasional discovery pop can occur well down the curve, as we have defined the peak in the early 1960's.

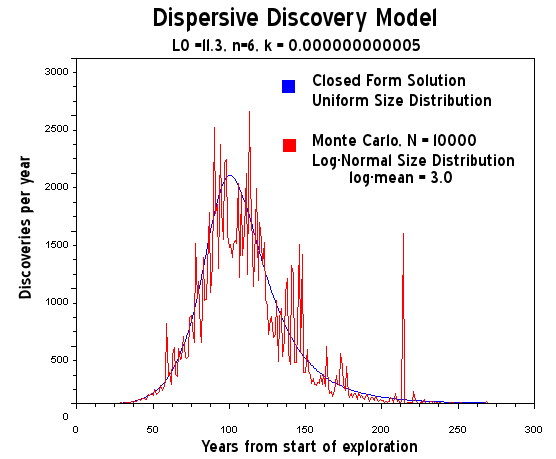
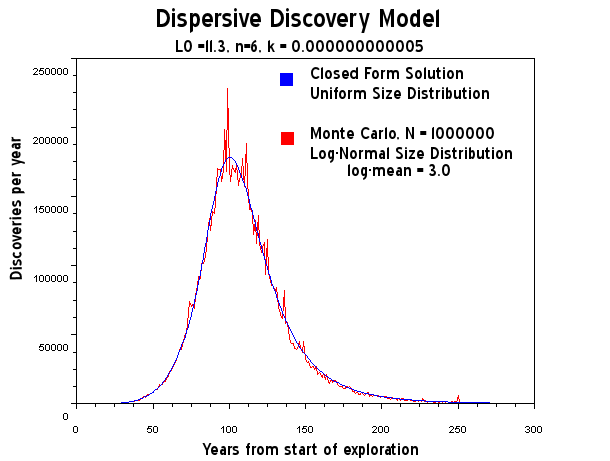
Figure 4: A discrete Monte Carlo simulation of dispersive oil discovery which shows both the statistical fluctuations and the sparseness of the finds down the tail of the curve. With more data sample the fluctuations diminish in size.

So contrary to recent activity of huge new discoveries as reported by the NY Times, the days of sustained discoveries remain behind us and we are seeing the occasional pop of the popcorn.

---

Ugo Bardi at TOD had posted a suggestion that we come up with a "mind-sized model" to described the Hubbert Peak. This makes a lot of sense as we still have the problem of trying to convince politicians and ordinary citizens of what constitutes the issue of peak oil and more generally peak oil.

Why we try to do this has some psychological basis. This last week, I worked on some ideas pertaining to the technique of Design of Experiments, and a colleague had turned me on to an in-house course on the topic. There, in the course notes introduction, the instructor had laid out the rules essentially describing the three stages of learning. The bullet points pointed out that understanding did not come about instantaneously, and instead progressed through various psychological stages. I figured that he did this as a precaution to not wanting to frighten his students at the level of effort required in learning the subject material. This explanation basically amounted to a cone of experience conceptual model, with a progression through the stages of enactive, iconic, and symbolic learning. Enactive amounts to a type of hands-on learning through first-hand experience; iconic boils it down to a psychological connection to the material via shared experience; and symbolic brings it to the level of analogies and potentially mathematics for the sophisticated learner.

The fundamental problem with understanding peak oil is that the enactive first-person learning and ultimately iconic shared experience only occurs on the most abstract level. We just cannot comprehend the global scope of the problem and can only reduce it to our day-to-day interactions and what we see at a local level. Therefore, only when we experience, or hear about something like gas station queues and price hikes do we make a connection to the overriding process at work. But these observations serve merely as side-effects and do not ultimately explain the bigger picture of oil depletion. In Bardi's view, it does not represent a good mind's eye view of peak oil.

Bardi tried to do this by comparing oil depletion to a Lotka-Volterra (L-V) model of predator-prey interactions. This works on all three levels, culminating in an abstraction that demonstrates the Hubbert Curve in mathematical curves. That would work perfectly ... if it actually modeled the reality of the situation. Unfortunately Bardi's L-V doesn't cut it and it will actually misrepresent our continued understanding of the situation. In other words, we cannot use Bardi's analysis as a tool for practicing depletion management. Our learning basically ends up in an evolutionary dead-end, and even though it effectively works on an emotional and psychological level to fill in our cone of experience, it misses the mark completely on mathematical correctness.

Other people try to make the symbolic connection by comparing the oil discovery process as searching through a pile of peanuts or cashews for edible pieces. This works on a qualitative level, but until we have some quantitative aspects, it ends up short on the symbolic mathematical level. I myself have used the analogy of finding needles in the haystack, which brings in the formal concepts of dispersion. The idea of popcorn popping fills in more of the enactive and iconic levels of our experience (who hasn't waited in agonizing expectation of the furtive last few pops?) and the experiments themselves demonstrate the symbolic math involved -- the process of accelerating discovery as our reserve bag of popcorn inflates, followed by a peak in maximum discoveries, followed by a slow decline as the most stubborn kernels pop. The production cycle culminates as we consume the popped popcorn at a later date.

To compare this understanding against Bardi's Lotka-Volterra or of the Verhulst formulations shows the limitations of the the predator prey model, as it simply does not take into account the stochastic environment of exploration. For example, what if we had applied an L-V formulation to the popcorn experiment, what would we get? Since it is deterministic, it would come out like a spike with the cumulative showing as a step function. All the L-V can do is work on the mean value, so that it misses the real dynamics of random effects. With L-V, all the popcorn would pop at the same time. This is as ridiculously simplistic an assumption as the spherical cow.

Moreover, the L-V model also assumes that some collective feedback plays a large role, as if the amount we have found or the amount remaining (as to in the Verhulst equation) determines the essentials of how depletion comes about. Yet, as the single kernel popcorn experiment bears out, the feedback term does not really exist. All we really have to understand is that certain stubborn pockets will remain and we need to keep accelerating our search if we want to maintain the Hubbertian Logistic-like shape. In other words, the natural shape does not decline as some intrinsic collective property. On an iconic level, the popcorn kernels that have popped don't tell their buddy kernels to stop popping once the bag is nearing completion. Yet, the predator-prey model tells us that is the reality and Bardi wants us to believe that interaction happens. That essentially what I want to get across: a real understanding of the situation.

So in effect, with the correct mathematical model, I could easily work out the popcorn dynamics from first principles and use that as a predictive tool for some future need (maybe I could go work for Orville Redenbacher). Or on a symbolic level, I would tell a politician that I could accurately gauge how long popcorn would take to pop and use that information to convince him that we could gauge future oil depletion dynamics. Unless he had never seen a popcorn popper in action (GHWB perhaps?) he would say, yeah that would make sense -- and then I could relate that to how it makes sense in how oil depletion dynamics plays out.

This is the kind of mind-sized model that we have just worked out.

---

Notes
[1] Apparently high school and college science teachers like to use popcorn popping experiments as a way to introduce the procedures of statistical data collection and the scientific method.

[2] A fixed exit criteria is like the finish line in a race (see below). A random exit criteria is where the finish line varies.