Ultimately we could consider knowledge as a survival tactic -- which boils down to the adage of eat or be eaten. If I want to sound even more pedantic, I would suggest that speed or strength works to our advantage in the wild but does not translate well to our current reality. It certainly does not work in the intentionally complex business world, or even with respect to our dynamic environment, as we cannot outrun or outmuscle oil depletion or climate change without putting our thinking hats on.
This of course presumes that we know anything in the first place. Nate Hagens had posted on TOD earlier this year the topic
"I Don't Know". I certainly don't profess to have all the answers, but I certainly want to know enough not to get crushed by the BAU machine. So, in keeping with the traditions of the self-help movement, we first admit what we don't know and build from there. That becomes
part of the scientific method, which a
few of us want to apply.
As a rule, I tend to take a nuanced analytical view to the way things may play out. I will use models of empirical data to understand nagging issues and stew over them for long periods of time. The stewing is usually over things I don't know. Of course, this makes no sense for timely decision making. If I morphed into a Thompson's gazelle with a laptop cranking away on a model under a shady baobob tree on the Serengeti, I would quickly get eaten. I realize that such a strategy does not necessarily sound prudent or timely.
Nate
suggests that the majority of people use fast and frugal heuristics to make day-to-day decisions (the so-called
cheap heuristic that we all appreciate). He has a point in so far as not always requiring a computatonal model of reality to map our behaviors or understanding. As Nancy Cartwright noted:
This is the same kind of conclusion that social-psychologist Gerd Gigerenzer urges when he talks about “cheap heuristics that make us rich.” Gigerenzer illustrates with the heuristic by which we catch a ball in the air. We run after it, always keeping the angle between our line of sight and the ball constant. We thus achieve pretty much the same result as if we had done the impossible—rapidly collected an indefinite amount of data on everything affecting the ball’s flight and calculated its trajectory from Newton’s laws.
This points out the distinction between conventional wisdom and knowledge. A conventionally wise person will realize that he doesn't have to hack some algorithm to catch a ball. A knowledgeable person will realize that he can (if needed) algorithmically map a trajectory to know where the ball will land. So some would argue that, from the point of timely decision making, whether having extra knowledge makes a lot of sense. In many cases, if you have some common sense and pick the right conventional wisdom, it just might carry you in your daily business.
But then you look at the current state of financial wheeling-dealings. In no way will conventional wisdom help guide us through the atypical set of crafty financial derivatives (unless you stay away from it in the first place).
Calvin Trillin wrote recently in the NY Times that the prospect of big money attracted the smartest people from the Ivy Leagues to Wall Street during the last two decades, thus creating an impenetrable fortress of opaque financial algorithms, with the entire corporate power structure on board. Trillin contrasted that to the good old days, where most people aiming for Wall St careers didn't know much and didn't actually try
too hard.
I reflected on my own college class, of roughly the same era. The top student had been appointed a federal appeals court judge — earning, by Wall Street standards, tip money. A lot of the people with similarly impressive academic records became professors. I could picture the future titans of Wall Street dozing in the back rows of some gut course like Geology 101, popularly known as Rocks for Jocks.
I agree with Trillin that the knowledge structure has become inverted; somehow the financial quants empowered themselves to create a world where no one else could gain admittance. And we can't gain admittance essentially because we don't have the arcane knowledge of Wall Street's inner workings. Trillin relates:
"That’s when you started reading stories about the percentage of the graduating class of Harvard College who planned to go into the financial industry or go to business school so they could then go into the financial industry. That’s when you started reading about these geniuses from M.I.T. and Caltech who instead of going to graduate school in physics went to Wall Street to calculate arbitrage odds."
“But you still haven’t told me how that brought on the financial crisis.”
“Did you ever hear the word ‘derivatives’?” he said. “Do you think our guys could have invented, say, credit default swaps? Give me a break! They couldn’t have done the math.”
If you can believe this, it appears that the inmates have signed a rent-controlled lease on the asylum and have created a new set of rules for everyone to follow. We have set in place a permanent thermocline that separates any new ideas from penetrating the BAU of the financial industry.
I need to contrast this to the world of science, where one can ague that we have more of a level playing field. In the most pure forms of science, we accept, if not always welcome, change in our understanding. And most of our fellow scientists won't permit intentional hiding of knowledge. Remarkably, this happens on its own, largely based on some unwritten codes of honor among scientists. Obviously some of the financial quants have gone over to the dark side, as Trillin's MIT and Caltech grads do not seem to share their secrets too readily. By the same token, geologists who have sold their soul to the oil industry have not helped our understanding either.
Given all that, it doesn't surprise me that we cannot easily convince people that we can understand finance or economics or even resource depletion like we can understand other branches of science. Take a look at any one of the
Wilmott papers featuring negative probabilities or Ito calculus, and imagine a quant using the smokescreen that "you can't possibly understand this because of its complexity". The massive pull of the financial instruments, playing out in what
Steve Ludlum calls the finance economy, does often make me yawn in exasperation out of the enormity of it all. Even the domain of resource depletion suffers from a sheen of complexity due to its massive scale -- after all, the oil economy essentially circles the globe and involves everyone in its network.
Therein lies the dilemma: we want and need the knowledge but find the complexity overbearing. Thus the key to applying our knowledge: we should not fear complexity, but embrace it. Something might actually shake out.
The word complexity, in short order, becomes the sticking point. We could perhaps get the knowledge but then cannot breech the wall of complexity.
I recently came across a description of the tug-of-war between complexity and simplicity when I happened across a provocative book called
"The Quark and the Jaguar : Adventures in the Simple and the Complex" by the physicist Murray Gell-Mann. I discovered this book while researching the
population size distribution of cities. One population researcher,
Xavier Gabaix, who I believe has a good handle on why Zipf's law holds for cities, cites Gell-Mann and his explanation of power laws. Gell-Mann's book came out fifteen years ago but it contains a boat-load of useful advice for someone that wants to understand how the world works (pretentious as that may sound).
I can take a couple of bits of general advice from Gell-Mann. First, when a behavior gets too complex, certain aspects of the problem
can become more simple. We can rather counter-intuitively actually simplify the problem statement, and often the solution. Secondly, when you peel the onion, everything can start to look the
same. For example, the simplicity of many power-laws may work to our advantage, and we can start to apply them to map much of our current understanding
2. As Gell-Mann states concerning the study of the simple and complex in the preface to the book:
It carries with it a point of view that facilitates the making of connections, sometimes between facts or ideas that seem at first glance very remote from each other. (Gell-Mann p. ix)
He calls the people that practice this approach "Odysseans" because they "integrate" ideas from those who "favor logic, evidence, and a dispassionate weighing of evidence", with those "who lean more toward intuition, synthesis, and passion" (Gell-Mann p.
xiii). This becomes a middle ground for Nate's intuitive cognitive (belief system) approach and my own practiced analysis. Interesting in how Gell-Mann moved from Caltech (one of Trillin's sources for wayward quants) to co-founding the Santa Fe Institute where he could pursue out-of-the-box ideas
3. He does caution that at least some fundamental and basic knowledge underlines any advancements we will achieve.
Specialization, although a necessary feature of our civilization, needs to be supplemented by integration of thinking across disciplines. One obstacle to integration that keeps obtruding itself is the line separating those who are comfortable with the use of mathematics from those who are not. (Gell-Mann p.15)
I appreciate that Gell-Mann does not treat the soft sciences as beneath his dignity and he seeks an understanding as seriously as he does deep physics. He sees nothing wrong with the way the softer sciences should work in practice, he just has problems with the current practitioners and their methods (some definite opinions that I will get to later).
For now, I will describe how I use Gell-Mann and his suggestions as a guide to understand problems that have confounded me. His book serves pretty well as a verification blueprint for the way that I have worked out my analysis. As it turns out, most of what Gell-Mann states regarding complexity I happily crib from, and allows me to use an
appeal to authority card to rationalize my understanding. (For this TOD post I was told to not use math and since Gell-Mann claims that his book is "comparatively non-technical", I am obeying some sort of transitive law
4 here) As a warning, since Gell-Mann deals first and foremost in the quantum world, his ideas don't necessarily come out intuitively.
That becomes the enduring paradox -- simplicity does not always relate to intuition. This fact weighs heavily on my opinion that cheap heuristics likely will not provide the necessary ammunition that we will need to make policy decisions.
BAU (business as usual) ranks as the world's most famous policy heuristic. A heuristic describes some behavior, and a simple heuristic describes it in the most concise language possible. So, BAU says that our environment will remain the same (as Nate would say "when NOT making a decision IS making a decision"). Yet we all know that this does not work. Things will in fact change. Do we simply use another heuristic? Let's try dead reckoning instead. This means that we plot the current trajectory (as Cartwright stated) and assume this will chart our course for the near future. But we all know that that doesn't work either as it will project CERA-like optimistic and never-ending growth.
Only the correct answer, not a heuristic, will effectively guide policy. Watch how climate change science works in this regard, as climate researchers don't rely on the Farmer's Almanac heuristics to predict climate patterns. Ultimately we cannot disprove a heuristic -- how can we if it does not follow a theory? -- yet we can replace it with something better if it happens to fit the empirical data. We only have to admit to our sunk cost investment in the traditional heuristic and then move on.
In other words, even if you can't "follow the trajectory" with your eye, you can enter a different world of abstraction and come up with a simple, but perhaps non-intuitive, model to replace the heuristic. So we get some simplicity but it leaves us without a perfectly intuitive understanding. The most famous example that Gell-Mann provides involves Einstein's reduction of Maxwell's four famous equations in complexity by 1/2 to two short concise relations; Einstein accomplishes this by invoking the highly non-intuitive notion of the space-time continuum. Gell-Mann specializes in these abstract realms of science, yet uses concepts such as "coarse graining" to transfer from the quantum world to the pragmatic tactile world, with the name partially inspired by the idea of a grainy photograph (Gell-Mann p.29). In other words, we may not know the specifics but we can get the general principles, like we can from a grainy photograph.
Hence, when defining complexity it is always necessary to specify a level of detail up to which the system is described, with finer details being ignored. (Gell-Mann p.29)
The non-intuitive connection that Gell-Mann triggers in me involves the use of probabilities in the context of disorder and randomness. Not all people understand probabilities, and in particular how we apply them in the context of statistics and risk (except for sports betting of course) , yet they don't routinely get used in the practical domains that may benefit from their use. How probabilities work in terms of complexity I consider mind-blowingly simple, primarily due to our old friend Mr. Entropy.
Never mind that entropy ranks as a most anti-intuitional concept.
SIMPLICITY
Reading Gell-Mann's book, I became convinced that applying a simple model should not immediately raise suspicions. Lots of modeling involves building up an artifice of feedback-looped relationships (see the Limits to Growth system dynamics model for an example), yet that should not provide an acid test for acceptance. In actuality, the large models that work consist of smaller models built up from sound principles, just ask Intel how they verify their microprocessor designs.
My approach consists of independent research and then forays into what I consider equally simple connections to other disciplines, essentially the Odyssean thinking that Gell-Mann supports.
I would argue that the fundamental trajectory of oil depletion provides one potentially simplifying area to explore. I get the distinct feeling that no one has covered this, especially in terms of exactly
why the classical heuristic, i.e. Hubbert's logistic curve, often works. So I have merged that understanding with the fact that I can use it to also understand related areas such as:
- Popcorn popping times
- Anomalous transport
- Network TCP latencies
- Reserve growth
- Component reliability
- Fractals and the Pareto law
I collectively use these to support the
oil dispersive discovery model -- yet it does bother me that no one has happened across this relatively simple probability formulation. You would think someone would have discovered all the basic mathematical principles over the course of the years, but apparently this one has slipped through the cracks.
Gell-Mann predicted in his book that this unification among concepts would occur if you continue to peel the onion. To understand the basics behind the simplicity/complexity approach, consider the complexity of the following directed graphs of interconnected points. Gell-Mann asks us which graphs we would consider simple and which ones we would consider complex. His answer relates to how compactly or concisely we can describe the configurations. So even though (A) and (B) appear simple and we can describe them simply, the graph in (F) borders on ridiculously simple, in that we can describe it as "all points interconnected". So this points to the conundrum of a complex, perhaps highly disordered system, that we can fortunately describe very concisely. As humans, the fact that we can do some pattern recognition allows us to actually discern the regularity from the disorder.
Figure 1: Gell-Mann's connectivity patterns.
However, what exactly the pattern means may escape us. As Gell-Mann states:
We may find regularities, predict that similar regularities will occur elsewhere, discover that the prediction is confirmed, and thus identify a robust pattern: however, it may be a pattern that eludes us. In such a case we speak of an "empirical" or "phenomenological" theory, using fancy words to mean basically that we see what is going on but do not yet understand it. There are many such empirical theories that connect together facts encountered in everyday life. (Gell-Mann p.93)
That may sound a bit pessimistic, but Gell-Mann gives us an out in terms of always considering the concept of entropy and applying the second law of thermodynamics (the disorder in an isolated system will tend to increase over time until it reaches an equilibrium). Many of the pattens such as the graph in Figure 1(F) have their roots in disordered systems. Entropy essentially quantifies the amount of disorder, and that becomes our "escape hatch" in how to simplify our understanding.
In fact, however, a system of very many parts is always described in terms of only some of its variables, and any order in those comparatively few variables tends to get dispersed, as time goes on, into other variables where it is no longer counted as order. That is the real significance of the second law of thermodynamics. (Gell-Mann p.226)
One area that I have recently applied this formulation to has to do with the distribution of human travel times.
Brockmann et al reported in
Nature a few years ago a scalability study that provoked some scratching of heads (one follow-on paper asked the questions
"Do humans walk like monkeys?"). The data seemed very authentic as at least one other group could reproduce and better it, even though they could not explain the mechanism. The general idea, which I have further described
here, amounts to nothing more than tracking individual travel times over a set of distances, and thus deriving statistical distributions of travel time by either following the cookie trails of paper money transactions (Brockmann) or cell phone calls (
Gonzalez). This approach provides a classic example of a "proxy" measurement; we don't measure the actual person with sensors but we use a very clever approximation to it. Proxies can take quite a beating in other domains, such as
historical temperature records, but this set of data seems very solid. You will see this in a moment.
 Figure 2:
Figure 2: Human travel connectivity patterns, from Brockmann, et al.
Note that this figure resembles the completely disordered directed graph shown by Figure 1(f). This gives us some hope that we can actually derive a simple description of the phenomenon of travel times. We have the data, thus we can hypothetically explain the behavior. As the data has only become available recently, likely no one has thought of applying the simplicity-out-of-complexity principles that Gell-Mann has described.
So how to do the reduction
5 to first principles? Gell-Mann brings up the concept of entropy as ignorance. We actually don't know (or remain ignorant of) the spread or dispersion of velocities or waiting times of individual human travel trajectories, so we do the best we can. We initially use the hint of representing the aggregated travel times -- the macro states -- as coarse-grained histories, or mathematically in terms of probabilities.
Now suppose the system is not in a definite macrostate, but occupies various macrostates with various probabilities. The entropy of the macrostates is then averaged over them according to their probabilities. In addition, the entropy includes a further contribution from the number of bits of information it would take to fix the macrostate. Thus the entropy can be regarded as the average ignorance of the microstate within a macrostate plus the ignorance of the macrostate itself. (Gell-Mann p.220)

In the way Gell-Mann stated it, I interpret it to mean that we can apply the
Maximum Entropy Principle for probability distributions. In the simplest case, if we only know the average velocity and don't know the variance we can assume a damped exponential probability density function (PDF). Since the velocities in such a function follow a pattern of many slow velocities and progressively fewer fast velocities, but with the mean invariant, the unit normalized distribution of transit probabilities for a fixed distance looks like the figure to the right (see
link for derivation). To me it actually looks very simple, although people virtually never look at exponentials this way, as it violates their intuition. What may catch your eye in particular is how slowly the curve reaches the asymptote of 1 (which indicates a power-law behavior). If normal statistics acted on the velocities, the curve would look much more like a "step" function, as most of the transits would complete at around the mean, instead of getting spread out in the entropic sense.
Further since the underlying exponentials describe specific classes of travel, such as walking, biking, driving, and flying, each with their own mean, the smearing of these probabilities leads to a characteristic single parameter function that fits the data as precisely as one could desire. The double averaging of the microstate plus the macrostate effectively leads to a very simple scale-free law as shown by the blue and green maximum entropy lines I added in Figure 3.
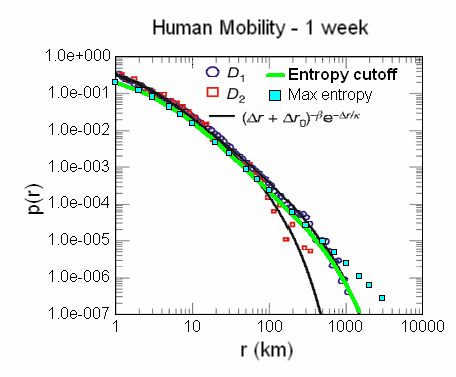
 Figure 3:
Figure 3: Dispersion of mobility for human travel. The green line indicates agreement with a truncated Maximum Entropy estimate, and the blue dots indicate no truncation
I present the complete derivation
here and the verification
here. If you decide to read in more depth, keep in mind that it really boils down to a single-parameter fit -- and this over a good 5 orders of magnitude in one dimension and 3 orders in the other dimension. Consider this agreement in the face of someone trying to falsify the model; they would essentially have to disprove entropy of dispersed velocities.
It has often been empasized, particularly by the philosopher Karl Popper, that the essential feature of science is that its theories are falsifiable. They make predictions, and further observations can verify those predictions. When a theory is contradicted by observations that have been repeated until they are worthy of acceptance, that theory must be considered wrong. The possibility of failure of an idea is always present, lending an air of suspense to all scientific activity. (Gell-Mann p.78)
Further, this leads to a scale-free power law that looks exactly like the Zipf-Mandelbrot law that Gell-Mann documents, which also describes ecological diversity (the
relative abundance distribution) and the
distribution of population sizes of cities, from which I found Gell-Mann in the first place.
Since we invoke the name of Mandelbrot, we need to state that the observation of fractal self-similarity on different scales applies here. Yet Gell-Mann states:
Zipf's law remains essentially unexplained, and the same is true of many other power laws. Benoit Mandelbrot, who has made really important contributions to the study of such laws (especially their connection to fractals), admits quite frankly that early in his career he was successful in part because he placed more emphasis on finding and describing the power laws than on trying to explain them (In his book The Fractal Geometry of Nature he refers to his "bent for stressing consequences over causes."). (Gell-Mann p.97)
Gell-Mann of course made this statement before
Gabaix came up with his own proof for city size, and obviously before I presented the variant for human travel (not that he would have read my blog or this blog in any case).
Barring the fact that it hasn't gone through a rigorous scientific validation, why does this formulation seem to work so well at such a concise level? Gell-Mann provides an interesting sketch showing how order/disorder relates to effective complexity, see Figure 4 below. At the left end of the spectrum, where minimum disorder exists, it takes very little effort to describe the system. As in Figure 1(a), "no dots connected" describes that system. In contrast, at the right end of the spectrum, where we have a maximum disorder, we can also describe the system very simply -- as in Figure 1(f), "all dots connected". The problem child exists in the middle of the spectrum, where enough disorder exists that it becomes difficult to describe and thus we can't solve the general problem easily.
Figure 4: Gell-Mann's complexity estimator. "the effective complexity of the observed system (can have) more to do with the particular observer's shortcomings than with the properties of the system observed." (Gell-Mann p.56)
So in the case of human transport, we have a simple grid where all points get connected (we can't control where cell phones go) and we have a maximum entropy in travel velocities and waiting times. The result becomes a simple explanation of the empirical Zipf-Mandelbrot Law [
wiki]. The implication of all this is that through the use of cheap oil for powering our vehicles, we as humans have dispersed almost completely over the allowable range of velocities. It doesn't matter that we have one car that is of a particular brand and that an airliner is prop or jet, the spread in velocities while maximizing entropy is all that matters. Acting as independent entities, we have essentially reached an equilibrium where the ensemble behavior of human transport obeys the second law of thermodynamics concerning entropy.
Entropy is a useful concept only when a coarse graining is applied to nature, so that certain kinds of information about the closed system are regarded as important and the rest of the information is treated as unimportant and ignored. (Gell-Mann p.371)
Consider one implication of the model. As the integral of the distance-traveled curve in Figure 3 relates via a proxy to the total distance traveled by people, the only direction that the curve can go in an oil-starved country is to shift to the left. Proportionally more people moving slowly means that fewer proportionally will move quickly -- easy to state but not necessarily easy to intuit. That is just the way entropy works.

Figure 5: Assuming that human travel statistics follows the maximum entropy velocity dispersion model, a reduction in total travel will likely result in a shift as shown by the dotted blue curve.
But that does not end the story. Recall that Gell-Mann says all these simple systems have huge amounts of connectivity. Since one disordered system can look like another, and as committed Odysseans, we can make many analogies to other related systems. He refers to this process as "peeling the onion". Figuratively as one can peel a particular onion, another layer can reveal itself that looks much like the surrounding layer. I took the dispersive travel velocities way down to the core of the onion in a study I did recently on
anomalous transport in semiconductors.
Often in physics, experimental observations are termed "anomalous" before they are understood.
-- Richard Zallen, "The physics of amorphous solids", Wiley-VCH, 1998
If you can stomach some serious solid-state physics take a peek at the results -- it's not like you will see the face of Jesus, but the anomalous behavior does not seem so anomalous anymore. Like Gell-Man states, these simple ideas connect all the way through the onion to the core.
SCALING
The big sweet Vidalia onion that I want to peel is oil depletion. All the other models I work out indirectly support the main premise and thesis. They range from the microscopic scale (semiconductor transport) to the human scale (travel times) and now to the geologic scale. I assert that in the Popper sense of falsifiability, one must disprove all the other related works to disprove the main one, which amounts to a scientific form of circumstantial evidence, not quite implying certainty but substantiating much of the thought process. It also becomes a nerve-wracking prospect; if one of the models fails, the entire artifice can collapse like a house of cards. Thus the "air of suspense to all scientific activity" that Gell-Mann refers to.
So consider rate dispersion in the context of oil discovery. Recall that velocities of humans become dispersed in the maximum entropy sense. Well, the same holds for prospecting for oil. I suggest that like human travel, all discovery rates have maximum dispersion subject to an average current-day-technology rate.
A real eye-opener to me occurred when I encountered Gell-Mann's description of depth of complexity. I consider this a rather simple idea because I had used it in the past, actually right here on TOD (see the post
Finding Needles in a Haystack where I called it "depth of confidence"). It again deals with the simplicity/complexity duality but more directly in terms of elapsed time. Gell-Mann explains the depth of complexity by invoking the "
monkeys typing at a typewriter" analogy. If we set a goal for the monkeys to type out the compleat works of Shakespeare, one can predict that due solely to probability arguments they would eventually finish their task. It would look something like the following figure with the depth
D representing a crude measure of generating the complete string of letters that comprises the text.
 Figure 6:
Figure 6: Gell-Mann's Depth (d) is the cumulative Probability (P) that one can
gain a certain level of information within a certain Time (T).
No pun-intended, Gell-Mann coincidentally refers to
D as a "crude complexity" measure; I use the same conceptual approach to arrive at the model of dispersive discovery of crude oil. The connection invokes the (1) dispersion of prospecting rates (varying speeds of monkeys typing at the typewriters) and (2) a varying set of sub-volumes (different page sizes of Shakespeare's works). Again, confirming the essential simplicity/complexity duality, the fact that we see a connectivity lies more in the essential simplicity in describing the disorder than anything else.

The final connection (3) involves the concept of increasing the average rate of speed of the typewriting monkeys over a long period of time. We can give the monkeys faster tools without changing the relative dispersion in their collective variability
6. If this increase turned out as an exponential acceleration in typing rates (see Figure 10), the shape of the
Depth curve would naturally change. This idea leads to the dispersive discovery sigmoid shape -- as our increasing prospecting skill analogizes to a speedier version of a group of typewriting monkeys. See the figure to the right for a Monte Carlo simulation of the monkeys at work [
link].
It doesn't matter that we have one oil reservoir that has a particular geology and that this somehow deflects the overall trajectory, as we would have to if we considered a complete bottom-up accounting approach. I know this may disturb many of the geologists and petroleum engineers who hold to the conventional wisdom about such pragmatic concerns, but that essentially describes how a thinker such as Gell-Mann would work out the problem. The crude complexity suggests that we turn technology into a coarse grained "fuzzy" measurement and accelerate it to see how oil depletion plays out. So if you always thought that the oil industry essentially flailed away like various monkeys at a typewriter, you would approximate the reality more so than if you believed that they followed some predetermined Verhulst-generated story-line. So this model embraces the complexity inherent of the bottom-up approach, but ignoring the finer details and dismissing out of hand that determinism plays a role in describing the shape.
Luis de Sousa gives a short explanation of how the deterministic Verhulst equation leads to the Logistic
here and it remains the conventional heuristic wisdom that one will find on
wikipedia concerning the Hubbert Peak Oil curve. However, Verhulst generated determinism does not make sense in a world of disorder and fat-tail statistics, as only stochastic measures can explain the spread in discovery rates. This becomes the mathematical equivalent of "not seeing the forest for the trees". Pragmatically, the details of the geology do not matter, just like the details of the car or bicycle or aircraft you travel in does not matter for modeling Figure 3.
This approach encapsulates the gist of Gell-Mann's insights on gaining knowledge from complex phenomena. His main idea is the astounding observation that complexity can lead to simplicity. I am starting to venture onto very abstract ice here, but the following figure represents where I think some of the models reside on the complexity mountain.
 Figure 7 :
Figure 7 : Abstract representation of our understanding of resource depletion.
Notice that I place the "Limits to Growth" System Dynamics model right in the middle of the meatiest complexity region. That model has perhaps too many variables and so will mine the swamps of complexity without adding much insight (or in more jaded terms, any insight that you happen to require). Many people assume that the Verhulst equation, used to model predator-prey relationships and the naive Hubbert formula of oil depletion, is complex since it describes a non-linear relation. However the Verhulst actually proves too simple, as it includes no disorder, and doesn't really explain anything but a non-linear control law. The only reason that it looks like it works is that the truly simple model has a fortuitous equivalence to the simplified-complex model
7, which exists as the dispersive discovery model on the other right-hand side of the spectrum. On the other hand, consider that the export land model (
ELM) remains simple and starts to include real complexity, approaching the bottom-up models that many oil depletion analysts typically use.
Further to the left, I suggest that the naive heuristics such as BAU and dead reckoning don't fit on this chart. They assume an ordered continuance of the current state, yet one can't argue heuristics in the scientific sense as they have no formal theory to back them up
8. The complementary effect way to the right suggests enough disorder that we can't even predict what may happen, the so-called
Black Swan theory proposed by Taleb.
On the bulk of the right side, we have all the dispersive models that I have run up the flag-pole for evaluation. These all basically peel the onion, and follow Gell-Mann's suggestion that all reductive fundamental behaviors will show similarities at a coarse graining level. This includes one variation that refer to as the
dispersive aggregation model for reservoir sizing. This has some practicality for estimating URR and it comes with its own linearization technique along the same lines as Hubbert Linearization (HL). You may ask if this is purely an entropic system, why would reservoirs become massive?
Sometimes people who for some dogmatic reason reject biological evolution try to argue that the emergence of more and more complex forms of life somehow violates the second law of thermodynamics. Of course it does not, any more than the emergence of more complex structures on a galactic scale. Self-organization can always produce local order. (Gell-Mann p.372)
Gell-Mann used the example of earthquakes and the relative scarcity of very large earthquakes to demonstrate how phenomenon can appear to "self-organize". Laherrere has used a
parabolic fractal law, a pure heuristic to model the sizing of reservoirs (and eathquakes), whereas I use the simple dispersive model as shown below.

Figure 8 : Dispersed velocities suggests a model of aggregation, much like Gabaix suggests for aggregation of cities. Very few large reservoirs and many small ones, just as in the distribution of cities.
These dispersive forms all fit together tighter than a drum. That essentially explains why I think we can use simple models to explain complex systems. I admit that I have tried to take this to some rather unconventional analogies, yet it seems to still work. I keep track of these models on this here blog.
Figure 9 : Popcorn popping kinetics follows the same dispersive dynamics [
link].
DISCUSSION
I found many other insights in Gell-Mann's book that expand the theme of this post and so seem worthwhile to point out. I wrote this post with the intention of referencing Gell-Mann heavily because many of the TOD comments in the past have criticized not incorporating a popular science angle to the discussion. I consider Gell-Man close to Carl Sagan in this regard (w/o the "billions" of course). I essentially used the book as an interactive guide, trying to follow his ideas by comparing them to models that I had worked on.
Evidently, the main function of the book is to stimulate thought and discussion.
Running through the entire text is the idea of the interplay between the fundamental laws of nature and the operation of chance. (Gell-Mann p.367)
The role of chance, and therefore probabilities, seems to rule above all else. Not surprising from a quantum mechanic.
Gell-Mann has quite a few opinions on the state of multi-disciplinary research, with interesting insight in regards to different fields of study. He treats the problems seriously as he believes certain disciplines have an aversion to accommodating new types of knowledge. And these concerns don't sit in a vacuum, as he spends the last part of the book discussing sustainability and ways to integrate knowledge to solve problems such as resource depletion.
The lnformational Transition
Coping on local, national, and transnational levels with environmental and demographic issues, social and economic problems, and questions of international security as well as the strong interactions among all of them, requires a transition in knowledge and understanding and in the dissemination of that knowledge and understanding. We can call it the informational transition. Here natural science, technology behavioral science, and professions such as law, medicine, teaching, and diplomacy must all contribute, as, of course, must business and government as well. Qnly if there is a higher degree of comprehension, among ordinary people as well as elite groups, of the complex issues facing humanity is there any hope of achieving sustainable quality.
It is not sufficient for that knowledge and understanding to be specialized. Of course, specialization is necessary today But so is the integration of specialized understanding to make a coherent whole, as we discussed earlier. It is essential, therefore, that society assign a higher value than heretofore to integrative studies, necessarily crude, that try to encompass at once all the important features of a comprehensive situation, along with their interactions, by a kind of rough modeling or simulation. Some early examples of such attempts to take a crude look at the whole have been discredited, partly because the results were released too soon and because too much was made of them. That should not deter people from trying again, but with appropriately modest claims for what will necessarily be very tentative and approximate results.
An additional defect of those early studies, such as Limits to Growth, the first report to the Club of Rome, was that many of the critical assumptions and quantities that determined the outcome were not varied parametrically in such a way that a reader could see the consequences of altered assumptions and altered numbers. Nowadays, with the ready availability of powerful computers, the consequences of varying parameters can be much more easily explored. (Gell-Mann p. 362)
Gell-Mann singles out geology, archaelogy, cultural anthropology, most parts of biology for criticism, and many of the softer sciences, not necessarily because the disciplines lack potential, but because they suffer from some massive sunk-cost resistance to accepting new ideas. He gives the example of distinguished members of the geology faculty of Caltech
"contemptuosly rejecting the idea of continental drift" for many years into the 1960's (Gell-Mann p. 285). This extends to beyond academics, as I recently I came across some serious arguments about whether geologists actually understand the theory behind
geostatistics and the use of a technique called "kriging" to estimate mineral deposits from bore-hole sampling (just reporting the facts). And then Gell-Mann relates this story on practical modeling within the oil industry:
Peter Schwartz, in his book "The Art of the Lonq Wew", relates how the planning team of the Royal Dutch Shell Corporation concluded some years ago that the price of oil would soon decline sharply and recommended that the company act accordingly The directors were skeptical, and some of them said they were unimpressed with the assumptions made by the planners. Schwartz says that the analysis was then presented in the form of a game and that the directors were handed the controls, so to speak, allowing them to alter, within reason, inputs they thought were misguided. According to his account, the main result kept coming out the same, whereupon the directors gave in and started planning for an era of lower oil prices. Some participants have a different recollections of what happened at Royal Dutch Shell, but in any case the story beautifully illustrates the importance of transparency in the construction of models, As models incorporate more and more features of the real world and become correspondingly more complex, the task of making them transparent, of exhibiting the assumptions and showing how they might be varied, becomes at once more challenging and more critical. (Gell-Mann p. 285)
Trying to understand why some people tend to a very conservative attitude, Gell-Mann has an interesting take on the word "theory" and the fact that theorists in many of these fields get treated with little respect.
"Merely Theoretical" -- Many people seem to have trouble with the idea of theory because they have trouble with the word itself, which is commonly used in two quite distinct ways. On the one hand, it can mean a coherent system of rules and principles, a more or less verified or established explanation accounting for know facts or phenomena. On the other hand, it can refer to speculation, a guess or conjecture, or an untested hypothesis, idea or opinion. Here the word is used with the first set of meanings, but many people think of the second when they hear "theory" or "theoretics". (Gell-Mann p.90)
Unfortunately, I do think that this meme that marginalizes peak oil "theory" will gain momentum over time. Particularly, in terms of whether peak oil theory has any real formality behind it, as certainly no one in academic geology besides Hubbert
9has really addressed the topic. Gell-Mann suggests that many disciplines simply believe that they don't need theorists. TOD commenter
SamuM provided some
well-founded principles to consider when mounting a theoretical approach, especially in responding to countervaling theories, i.e in debunking the debunkers. I am all for continuing this as a series of technical posts.
10 In the field of economics, Barry Ritholtz has also recently suggested a more scientific approach in The Hubris of Economists, yet he doesn't think that modeling necessarily works in economics (huh?). He might well consider that economics and finance modeling assumes absolutely no entropic dispersion. Taleb suggests that they should include fat-tails. The amount of effort placed in applying normal statistics has proven out as a colossal failure. We get buried daily in discussions on how to best to generate a course-correction within our economy, balanced between a distinct optimism and a bleak pessimism. At least part of the pessimism stems from the fact that we think the economy will forever stay coveniently complex beyond our reach. I would suggest that simple models may help just as well and that it allows us to understand when non-cheap heuristics and complex models woork against our best interests (i.e. when we have been played).
The "cost of information" addresses the fact that people may not know how to make reasonable free market decisions (for instance about purchases) if they don't have the necessary facts or insights. (Gell-Mann p.325)
Above all, Gell-Man asks the right questions and provides some advice on how to move forward..
If the curves of population and resource depletion do flatten out, will they do so at levels that permit a reasonable quality of human life, including a measure of freedom, and the persistence of a large amount of biological diversity, or at levels that correspond to a gray world of scarcity, pollution, and regimentation, with plants and animals restricted to a few species that co-exist easily with mankind? (Gell-Mann p.349)
We are all in a situation that resembles a fast vehicle at night over unknown terrain that is rough, full of gullies, with precipices not far off. Some kind of headlight, even a feeble and flickering one, may help to avoid some of the worst disasters. (Gell-Mann p.366)
I hope that I have illustrated how I have attempted to separate the simple from the complex. If this has involved too much math, I apologize.
I admit that we still don't understand econ though.
References
- Murray Gell-Mann, "The Quark and the Jaguar : Adventures in the Simple and the Complex", 1995, Macmillan
- Calvin Trillin, "Wall Street Smarts", NY Times, October 13, 2009
- Nassim Nicholas Taleb, "The Black Swan: The Impact of the Highly Improbable", 2007, Random House
- D. Brockmann, L. Hufnagel & T. Geisel, "The scaling laws of human travel", Nature, Vol 439|26, 2006.
- Marta C. González, César A. Hidalgo & Albert-László Barabási,, "Understanding individual human mobility patterns", Nature, Vol 453, 779-782 (5 June 2008).
Figure 10: A damped exponential contains a maximum entropy amount of information, such as the decay of radioactive material. The rising exponential usually occurs due to a degree of feedback reinforcing some effect, such as technology advances.
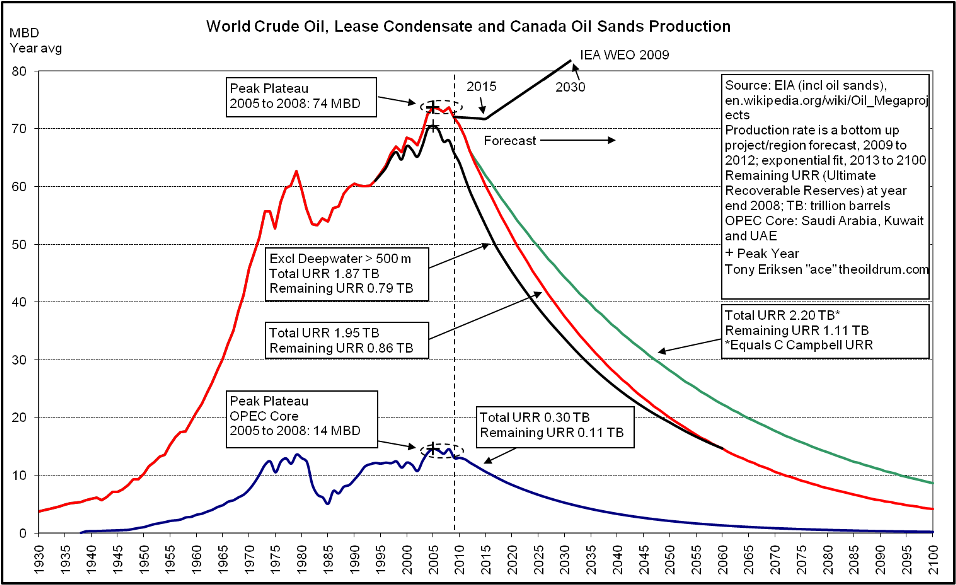 Ace pointed out the line labeled IEA WEO 2009 projects a stable or slightly falling crude output until 2015, after which it shows a slope change and starts a linear increase.
Ace pointed out the line labeled IEA WEO 2009 projects a stable or slightly falling crude output until 2015, after which it shows a slope change and starts a linear increase.