According to the
Oil Shock model, to first order the rate of depletion occurs proportionately to the amount of reserve available. Overall, this number has remained high and fairly constant (I consider 5% per year high for any non-renewable resource). It takes effort to extract it substantially faster than this, but because of oil's value -- they don't call it black gold for nothing -- we never have had a reason
not to extract, and so it has maintained its rate at a steady level, OPEC notwithstanding. And because the extraction rate has never varied by orders of magnitude, we have little insight into what we have in store for the future. In other words, can we actually pump faster?
The following proportionality equation forms the
lowest-level building block of the Shock model.
dU/dt = -k U(t)
Any shocks come about by perturbing the value of
k in the equation. Painfully stating the obvious, the values of
k can go up or down. Up to now the perturbations have usually spiked downward, usually from OPEC decisions. In particular, during the oil crises of the 1970's, the model showed definite glitches downward corresponding to temporary reductions in the extraction rate imposed to member countries by the cartel (of which formed the
original motivation and basis of the shock model).

The characteristic solution of the first-order equation to delta function initial conditions derives to a damped exponential.
U(t) = U0 e-kt
with extractive production following as the derivative of U(t) (the negative sign indicates extraction):
P(t) = -dU(t)/dt = k * U0 e-kt = k*U(t)
This gets back to the original premise:
"rate of depletion occurs proportionately to the amount of reserve available".
As Khebab
has pointed out via the Hybrid Shock Model (HSM), this gives the behavior that production always decreases, unless additional reserves get added (the extrapolation of future reserves is the key to HSM). And if we reside near the backside of a peak and without any newly-discovered additive reserves, it will go only one way ...
down.
Yet we know that plateauing of the peak will likely occur, at least at the start of any detectable decline. This will invariably come about from an increase in extraction from reserves. According to the shock model, this only increases if
k increases. We can model this straightforwardly:
dU/dt = -(k + ct) U(t)
Regrouping terms to integrate:
dU/U = -(k + ct)dt
ln(U) - ln(U0) = -(kt + ct2/2)
this results in
U = U0 e-(kt + ct2/2)
P(t) = (k + ct)* U0 e-(kt + ct2/2)

Notice how this gives a momentary plateau that soon gets subsumed by the relentless extractive force.
Instead of a 2
nd order increase, we can try adding an exponential increase in extraction rate:
dU/U = -(k + a*ebt)dt
ln(U) - ln(U0) = -(kt + a*ebt/b)
The solution to this results in a variation of the
Gompertz equation:
U = U0 e-(kt + a*ebt/b)
P(t) = (k+ a*ebt)U0 e-(kt + a*ebt/b)

The uptick of the plateau has now become more pronounced. Overgeneralizing, "we" can now "dial-in" the extension of the plateau "supply" by "adjusting" the extraction rate at an accelerating rate. I place air quotes around these terms because I have a feeling that (1) know one knows the feasibility of improved extractive technology and (2) it will eventually hit a hard downslope. Under the best circumstances we may prolong the plateau somewhat.

Conversely, assuming the conditions of a non-rate limited supply, oil producers can increase their output at the whim of political decisions. No one really understands the extent of this strategy; the producers who consider oil as a cash cow will not intentionally limit production, while those who emulate OPEC cartel practices will carefully meter output to meet some geopolitical aims. In this case, shareholders demanding the maximization of profit do not play a role.
So, what is the downside of increasing the extraction rate?
Answer: The downside is the downslope. Quite literally, upping the extraction rate under a limited supply makes the downslope that much more pronounced. The Gompertz shows a marked asymmetry that more closely aligns to exponential rise and collapse than the typical symmetric Hubbert curve.
A while back I discussed the possibility of reaching TOP (see
The Overshoot Point) whereby we keep trying to increase the extraction rate until the reserve completely dries up and the entire production collapses. The following curves give some pre-dated hypothetical curves for TOP. The graph on the right shows the extractive acceleration necessary to maintain a plateau. At some point the extraction rate needs to reach ridiculous levels to maintain a plateau, and if we continue with only a linear rate of increase it starts to give and the decline sets in. Clearly, this approach won't sustain itself. And if we stop the increase completely, the production falls precipitously (see the Exponential Growth + Limit curve above).
In summary, this part of the post essentially covers the same territory as my initial TOP discussion from a few years ago, but I tried to give it some mathematical formality that I essentially overlooked for quite a while.
Do we ever see the Gompertz curve in practice? I venture to guess that yes we have. Not a pleasant topic, but we should remind ourselves that fast developing extinction events may show Gompertz behavior. Oil depletion dynamics would play out similarly to sudden extinction dynamics,
if and only if we assume that oil production immediately succeeded discovery and the extraction rate then started to accelerate. Then when we look at an event like passenger pigeon population (
where very limited dispersion occurs), the culling production increases rapidly and then collapses as the population can't reproduce or adapt fast enough.
As a key to modeling this behavior, we strip out dispersion of discovery
completely, and then provide a discovery stimulus as a delta function. For passenger pigeons the discovery occurred as a singular event along the Eastern USA during colonial times. The culling accelerated until the population essentially became extinct in the late 1800's.
To verify this in a more current context, I decided to look at the vitally important worldwide phosphate production curve. Bart Anderson at the Energy Bulletin first
wrote about this last year and he provided some valuable plots courtesy of his co-author Patrick Déry. At that time,
I thought we could likely do some type of modeling since the production numbers seemed so transparently available. Gail at TOD
provided an updated report courtesy of James Ward which rekindled my interest in the topic. Witness that the search for phosphate started within a few decades of the discovery of oil in the middle 1800's. Therefore one may think the shape of the phosphate discovery curve might also follow a logistic like curve. But I contend that this does not occur because of accelerating extraction rates of phosphate leading to more Gompertz-like dynamics.
The first plot that provides quite a wow factor comes from phosphate production on the island of Nauru by way of Anderson and Déry.

Note that the heavy dark green line that I added to the set of curves follows a Gompertz function with an initial stimulus at around the year 1900, and an exponential increase after that point. The total reserve available defines the peak and subsequent decline. The long uptake and rapid decrease both show up much better with Gompertz growth than with the HL/Logistic growth. This does not invalidate the HL (of which
Dispersive Discovery model plays a key role), but it does show where it may not work as well.
Remember that all the phosphate on that island essentially became "discovered" as a singular event in 1900 (not hard to imagine for the
smallest independent republic in the world). Since that time, worldwide fertilizer production/consumption has
increased exponentially reaching values of 10% growth per year before
leveling off to 5% or less per year. Google
"rate of fertilizer consumption" to find more evidence.
As a result, fertilizer trade increased from about 2 million tons in 1950 to about 40 million tons in 1986.
Over this period, this rate compounds to 9% annually, clearly an exponential increase which menas that the phosphate component of fertilizer increased as well.
Then if you consider that most easily accessible phosphate discoveries occurred long ago, the role of Gompertz type growth becomes more believable
1. No producer had ever really over-extracted the phosphate reserves in the early years, as we would have had no place to store it, yet the growth continued as the demand for phosphate for fertilizer increased exponentially. So as the demand picked up, phosphate companies simply depleted from the reserves until they hit the diminishing return part of the curve. The producers can essentially pull phosphates out of the reserves as fast as they wanted, while oil producers became the equivalent of drinking a milkshake from a straw, as sucking harder does not help much.
For worldwide production of phosphates, applying the Gompertz growth from non-dispersive discoveries gives a more pessimistic outlook than what James Ward calculated. The following figure compares Ward's Hubbert Linearization against an eyeballed Gompertz fit. Note that both show a similar front part of the curve but the Gompertz declines much more rapidly on the backside. The wild production swings may come about from the effects of a constrained supply, something quite familiar to those following the stock market recently and the effects of constrained credit on speculative outlook.

So we have the good news and the bad news. First, the good news: oil production does not follow the Gompertz curve as of yet and we may not ever reach that potential given the relative difficulty of extracting oil at high rates. The fact that we have such a high dispersion in oil discoveries also means that the decline becomes mitigated by new discoveries. As for the bad news: easily extractable phosphate may have hit TOP. And we have no new conventional sources. And phosphate essentially feeds the world.
Read the rest of
Ward's post for some hope:
Perhaps the best way to frame the debate from here is to suggest that, like oil, the world has been endowed with a given quantity of “easy” phosphorus (e.g. rich island guano deposits in places like Nauru) that can be – and have been – mined quite rapidly, as well as a larger endowment of lower-grade phosphate rock. While the easy phosphate has passed its peak, the low-grade phosphate should be considered separately. Figure 3 shows an example forecast where the total area under both curves (equal to RURR) is 24.3 billion tonnes, but the “easy” phosphorus (purple) is 9 billion tonnes as in Figure 2. Assuming the production history is mostly related to easy phosphorus, the fitting parameters (a and k) for the “hard” phosphorus cannot be established. Therefore, the height and timing of the secondary peak are unpredictable.

1 For a quick-and-dirty way to gauge discovery events, I used Google to generate a histogram. I describe this technique
here and
here. For phosphates, the histogram looks like this:

Note the big spike in discoveries prior to 1900; recent large discoveries remain rare. Prospectors have long ago sniffed out most new discoveries.
Update:Sulfur Gompertz, used in fertilizer production as well:

from http://pubs.usgs.gov/of/2002/of02-298/of02-298.pdf, ref courtesy of
TOD.
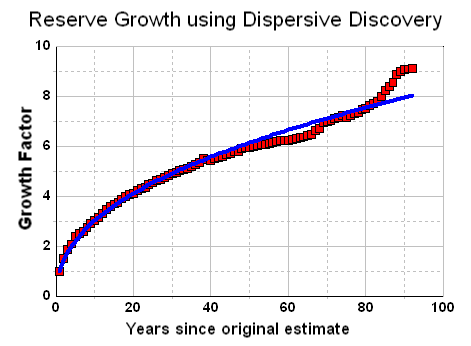



















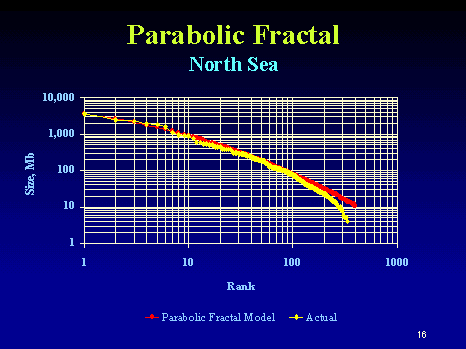
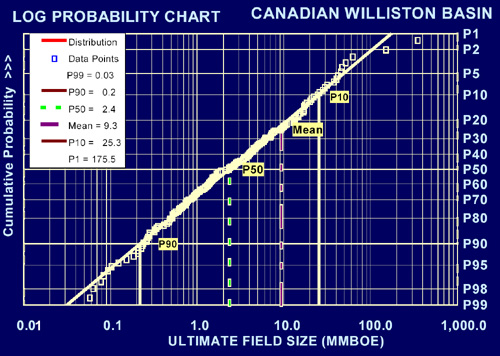 Neither the
Neither the 


 The characteristic solution of the first-order equation to delta function initial conditions derives to a damped exponential.
The characteristic solution of the first-order equation to delta function initial conditions derives to a damped exponential. 

 Conversely, assuming the conditions of a non-rate limited supply, oil producers can increase their output at the whim of political decisions. No one really understands the extent of this strategy; the producers who consider oil as a cash cow will not intentionally limit production, while those who emulate OPEC cartel practices will carefully meter output to meet some geopolitical aims. In this case, shareholders demanding the maximization of profit do not play a role.
Conversely, assuming the conditions of a non-rate limited supply, oil producers can increase their output at the whim of political decisions. No one really understands the extent of this strategy; the producers who consider oil as a cash cow will not intentionally limit production, while those who emulate OPEC cartel practices will carefully meter output to meet some geopolitical aims. In this case, shareholders demanding the maximization of profit do not play a role.

























