Hydrogeology for Dummies

A running theme of this blog involves the reduction of seemingly complex behaviors into simple mathematical formulations. It remains a bit of a mystery to me why in many situations that no one has either (a) done this work on their own or (b) uncovered the work of someone else who has done the simplifying analysis years ago.

The majority of scientists practicing mainstream research have furthered the cause by following the lead of others who go down blind alleys and over-complicate the analysis. I suspect that a few complicate matters intentionally, as it demonstrates to other scientists their intellectual prowess. In certain cases, creating a private world of intricate analysis acts as a kind of moat around which they can fortify their specialty discipline.

Of course, this doesn't happen universally. Certainly we run across many scientific and engineering subdisciplines that have gone through years of scrubbing. In these cases, the most salient and simple analyses have emerged and stood the test of time. They often share the same traits of elegance and crystalline transparency so that we can use their patterns to understand the world without a lot of extra effort. To me, that seems a reasonable goal to strive for.

In this post, I will go through the derivation of what I consider a very overlooked and simple argument having to do with the transport of materials in porous media -- much as what you would find in tracing a contaminant though a groundwater basin. Or what may happen if you frac for natural gas and open up new pathways to a drinking water aquifer. Or how oil will migrate to a reservoir over time, feeding the production output of a stripper well for years. Or what happens if you spill oil in a waterway.

Unfortunately, when you pose this kind of problem to a research geologist or hydrologist, you will have to prepare for an onslaught of ornate misdirection. They will either derive some hideous numerical model or possibly run a piece of commercial software. Apparently, they will never resort to plain logic and elementary first-principles considerations.

The Problem

1. Consider a contaminant that enters an aquifer in a single dose
2. Predict how long it will take to pass by a downstream location
3. How do you solve this problem?

A large scale experiment typically looks like this scenario:

from Groundwater Tracing in the Woodville Karst Plain

And you get a result that looks like the following figure. Intuitively, one would expect that the concentrated dose will disperse as it travels downstream and that the original concentration will spread out in time. The red curve that goes through the data gives you a feel for what I will derive via a simple model.

As a main premise, I assume that disorder plays a big role in providing a variety of pathways from source to sink. One can imagine that some paths might occur on the main waterway, providing a maximum speed or path of least resistance. Other paths may follow obstructions or diversions which will either slow down or speed up the flow from the main path.

The main path has a mean velocity v₀ and the other paths have probabilities that range below this, with some mean deviation v_m from v₀. A distribution that maximizes entropy while holding to these two minimal constraints looks like the following graph.

Figure 1: MaxEnt velocity distribution for absolute mean deviation

This illustrates simple dispersion. For this post we won't even consider diffusion, which although important may in fact act as only a second-order effect depending on the speed of the main flow.

The calculation of downstream concentration, n(x,t), drops out of the Fokker-Planck equation if we ignore diffusion. Note the delta function, δ(x-vt), which describes a traveling pulse for each velocity component.

n(x,t) = ∫ p(v) δ(x-vt) dv

Next we apply the Maximum Entropy Principle to generate a velocity distribution as shown in the Figure 1:

p(v) = 1/v_m exp(-|v-v_o|/v_m)

No other distribution has a higher entropy given that mean and an absolute deviation from the mean, so it ranks as the least biased estimator for that set of constraints. (Note that this does not describe the normal or Gaussian distribution as that requires a second-moment, i.e variance, constraint. It turns out that the mean deviation distribution, also known as the Laplace, is actually a smeared Gaussian where we have MaxEnt uncertainty in σ-squared. So Laplace entropy is higher than the Gaussian entropy)

We can trivially solve the integral to generate a concentration at some downstream location x (forget about adding extra dimensions as a one-dimensional result should suffice).

n(x,t) = 1/(v_mt) exp(-|x/(v_mt)-v₀/v_m|)

Let's see how this works in practice.

I pulled data from a pair of papers from 2008, "Non-Fickian dispersion in porous media", T Le Borgne, P Gouze, et al. The scientists created a carefully controlled experiment, which relied on a customized apparatus for making precise measurements of the contaminant, a flourescent dye called uranine. The value of this particular experiment lies in the large dynamic range of the resultant data. The concentration runs over 4-orders of magnitude and the time scale 2-orders. Their own model, although generating a good fit to the data, needed a numerical calculation to solve, violating my assertion that we can model via simpler mechanisms.

The following figure allows for the wide dynamic range by plotting the concentration (also known as a breakthrough curve) on a log-log scale. The red triangles ◊ fit the Maximum Entropy dispersion model, n(x,t), for a fixed value of x and a value of v_m/v₀ = 0.18. By inverting the concentration we can get the probability distribution of velocities in the bottom figure; on a semi-log plot a symmetric two-sided exponential looks like a perfect isosceles triangle. Based on the outstanding fit and symmetric distribution I find it blatantly obvious that entropic mechanisms generate the dispersion observed. You won't get this parsimonious a fit from such a simple model -- with essentially a single parameter v_m/v_{0 --} unless it has some real merit.

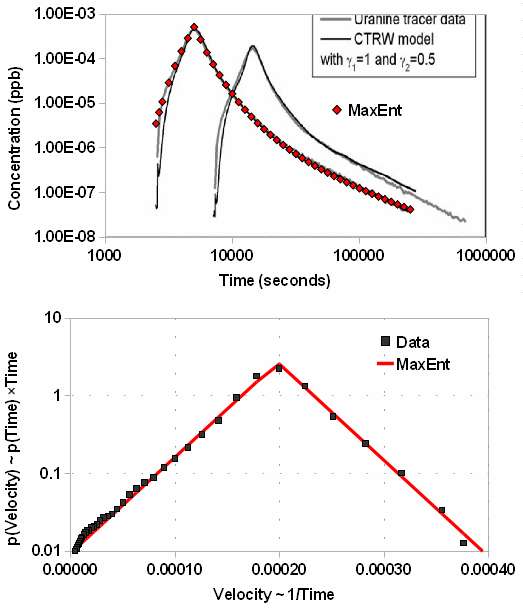Figure 2: Breakthrough curve (top) and
measured velocity distribution (bottom)
for flourescent dye tracer experiment.

I would suggest that any further modeling of these kinds of porous structures makes little sense since we have essentially proved that the multitude of the pathways maximize entropy and thus maximized the disorder of the system. In other words, you could not model a more complex system given those constraints if you tried. Nature will always win out with entropy in its back pocket.

The simplicity of the model also points out how readily fat-tail effects emerge from entropic disorder. The power law drop-off obeys a 1/time behavior that certainly has consequences in terms of how long a contaminant will remain in a groundwater basin. Velocity dispersion with a mean MaxEnt constraint will always lead to a power-law drop-off in time (see more here).

See also these posts:

1. http://mobjectivist.blogspot.com/2009/06/dispersive-transport.html
2. http://mobjectivist.blogspot.com/2010/05/characterizing-mobility-in-disordered.html
   
3. http://mobjectivist.blogspot.com/2010/05/fokker-planck-for-disordered-systems.html

The hydologists and geologists who ignore entropy in favor of some other fancy model do so based on their own stubborness or ignorance. I have observed the practice of making things too complicated runs rampant among geologists and it really strikes me as kind of sad. We have hydrogeologist hacks like Steven Gorelick writing cornucopian books diminishing the significance of peak oil, when they can't even do the science of their own discipline correctly.