Enclave

It figures that that the makers of the dying breed of vehicles known as SUV's have given one model the name Enclave.

enclave (n) : a distinct territorial, cultural, or social unit enclosed within or as if within foreign territory

Soon to come: the Garrison, the Fortress, the Anchor, the White Elephant.

The Shock Model in Action

Brown warns of global oil 'shock'


Radio talker Mike Malloy spent some time talking peak oil recently. As always, he had some interesting takes, especially concerning the religious right's belief in abundant oil. His response was "Well the Lord giveth, and the Lord taketh away".

Similar to what Aldo Leopold said: "the Lord giveth, and the Lord taketh away, but he is no longer the only one to do so."

Oil has become a despised personality

Jim Quinn, rabid right wing talk show host: "Somebody said this -- We can't make up for lack of oil by drilling more. That's as crazy as saying we can't make up a shortage of food by growing more"

Gold Rush dynamics, the Dispersive Discovery sanity check

Dynamics such as those that lead to extinction events and of boom-bust periods first motivated me to generalize discovery dynamics in terms of dispersive effects.

If we look into an extinction event such as passenger pigeons in the 1800's, we find a steadily accelerating harvest per year until culling hit a critical point and then fell precipitously. The harvests went spectacularly to zero and so, unfortunately, did the pigeon population.

I can say the same for boom-bust cycles, such as happened during the gold-rush days of the 1800's. In most cases, a boom occurred on the onset of an isolated discovery as many prospectors joined the search, enough time passed to enable the building of a huge infrastructure and then suddenly everything dried up with the infrastructure left standing in place.

But that hasn't happened with the discoveries of fossil fuel around the world. Although discoveries did increase at an accelerating pace until about the mid-part of the 20^the century, reaching a peak a little after 1960, many discoveries continue to occur and the bottom did not fall out, unlike the cases of extinction and nini-boom-busts. We explain this by considering the role of dispersion in the discoveries. The following figure shows a non-dispersed discovery function, which reaches a sharp peak and then drops to zero as prospectors finish searching an isolated volume of potential finds.



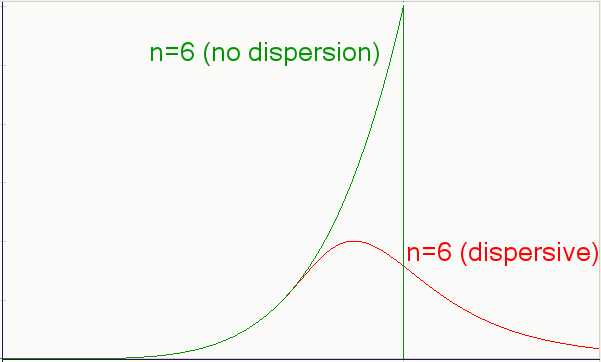
This basically happens when a highly localized search takes place, as with the case of the blanket coverage of passenger pigeon flyways with an efficient army of hunters (often equipped with explosives!). Its also happens with prospectors sifting everything with the equivalent of a fine-tooth comb in some localized gold strike area.

But the discovery of oil differs as dispersion in the rates of discovery in various parts of the world lead to a broad smearing of the bust peak. In fact, the effective bust peak (equal integrated volume) only lines up on the backside of the dispersed profile. This all makes consistent sense and provides a further argument against the use of the Logistic function to model any of these kinds of search processes, dispersed or not.

In other words someone has to explain why a symmetric Logistic function (ala the classic Hubbert curve) does not explain the steep drop-off displayed in many culling-forced extinction examples and of the bust drop-off in gold-rush cases.

Of course, this all gets the hand-wave treatment by the classically trained Hubbert modelers that use the Logistic function. Which I find really and truly odd as the Verhulst birth-death equations theoretically apply most effectively in localized Petri dish style experiments. Translation: analysis by Logistic approaches does not meet yet another sanity check and only serves as a cheap heuristic.

The Sigmoid Fraud

Unlike Sigmund Freud, I don't do psychology as a career but I do see something seriously disturbing about the fact that a majority of depletion analysts view the Logistic Function as something that contains some deep and significant meaning.

On the contrary, the Sigmoid curve --as the simplest manifestation of the Logistic-- remains a cheap empirical relationship that describes a value that increases and then saturates below some constrained limit. It indeed does follow from the solution of a non-linear differential equation, but this equation describes the temporal dynamics of a simplistic birth-death model used to describe interacting entities. One can choose populations of biological creatures or concentrations of chemical reagents to plug in to the equation. But you don't insert oil molecules into the equation and expect it to make any sense.

Take a look at this post at TOD on whale oil harvesting in the 1800's. Although the original poster does not bring up the Logistic to describe the saturation, plenty of commenters do. Fair enough, whales do fall into a biological classification, and they do give birth and die. But whale oil harvesting never tracked a population rise in whales themselves. It actually tracked the reverse. So, instead of calling it a "birth-death" model we should refer to it as a "death-birth" model. The parameter "death" represents the culling of the whale population for oil and any residual "birth" comes about because the whales can reproduce themselves based on the size of their population. Then as an exercise for the reader, one can plug some values into the birth-death equations as described here: Derivation of Logistic Growth.

But then we get to the real twist. Since whales do reproduce, if we play our cards right, then the amount of whale oil that we can harvest has no limit! The URR of whale oil essentially becomes infinite since the cumulative never abates. And unless we harvest the whales to extinction, the Logistic Function will fail miserably in describing whale oil production. (In actuality, cumulative whale oil production likely saturated because crude oil replaced whale oil as a harvestable resource.) See passenger pigeons if you want to get closer to a saturated harvest driven to extinction.

This whole analysis when incorrectly applied to oil exploration and production can induce early psychosis. On the one hand, oil does not reproduce like a biological entity nor does it act like a chemical reagent. So the equations themselves make no sense. But since oil only gets consumed and obeys the rules of a finite resource (abiotic-oil-mental-midgets notwithstanding), it will eventually saturate. So the Sigmoid falls into our lap in spite of itself. The fraud survives in effect only because it looks like an S-curve !

To avoid this mental anguish, I prefer to use the Dispersive Discovery formulation for discoveries and the Oil Shock model for extraction/production dynamics. This approach makes intuitive sense, the math falls out naturally, and you don't have to continue to psychoanalyze insane ramblings of people that live in some freakish world where square pegs fit into round holes and empiricism has the dynamic range of a stupid heuristic. The rise and fall of the oil culture deserves a better understanding than the Logistic can ever offer.

End promised rant;

Same: More Of

Kevin Phillips

What more can I say but that the inflation numbers and the dynamics therein remind me a lot about the essentially corporate and government cover-up behind the truth in oil reserves. We can easily figure this out if we had more committed and numerate people.

Unless you believe that growth consists in how many songs you can put into an mp3 player or the accelerating absurdity of Grand Theft Auto, money doesn't buy as much as it used to.