Rayleigh Fading, Wireless Gadgets, and a Global Context

The intermittent nature of wind power that I recently posted on has a fundamental explanation based on entropy arguments. It turns out that this same entropy-based approach explains some other related noisy and intermittent phenomena that we deal with all the time. The obvious cases involve the use of mobile wireless gadgets such as WiFi devices, cell phones, and GPS navigation aids in an imperfect (i.e. intermittent) situation. The GPS behavior has the most interesting implications which I will get to in a moment.

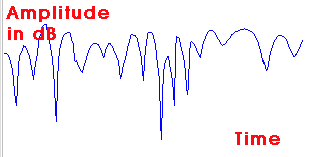
First of all, consider that we often use these wireless devices in cluttered environments where the supposedly constant transmitted power results in frustrating fade-outs that we have all learned to live with. An example of Rayleigh fading appears to the right. You can find some signal interference-based explanations for why this happens, originating via the same intentional phase cancellations that occur in noise-cancelling headphones. For the headphones, the electronics flip the phase so all interferences turn destructive, but for wireless devices, the interferences turn random, some positive and some negative, so the result gives the random signal shown.

In the limit of a highly interfering environment the amplitude distribution of the signal shows a Rayleigh distribution, the same observed for wind speed.

p(r) = 2kr exp(-kr²)

Because all we know about our signal is an average power, it occurred to me that one can use Maximum Entropy Principles to estimate the amplitude from the energy stored in the signal, just like one can derive it for wind speed. So, as a starting premise, if we know the average power alone, then we can derive the Rayleigh distribution.

The following figure (taken from here) shows the probability density function of the correlated power measured from a GPS signal. Since power in an electromagnetic signal relates to energy as a flow of constant energy per unit time, then we would expect the energy or power distribution to look like a damped exponential, in line with the maximum entropy interpretation. And sure enough, it does exactly match a damped exponential (note that the Std Dev = Mean, a dead giveaway for an exponential distribution).

p(E) = k*exp(-kE)

Yet since power (E) is proportional to Amplitude squared (r ²), we can derive the probability density function by invoking the chain rule.

p(A) = p(E)*dE/dr = exp(-kr²) * d(r²)/dr = 2kr * exp(-kr²)

which precisely matches the Rayleigh distribution, implying that Rayleigh fits the bill as a Maximum Entropy (MaxEnt) distribution. So too does the uniformly random phase in the destructive interference process qualify as a MaxEnt distribution, which will range from 0 to 360 degrees (which gives an alternative derivation of Rayleigh). So all three of these distributions, Exponential, Rayleigh, and Uniform all act together to give a rather parsimonious application of the maximum entropy principle.

The most interesting implication of an entropic signal strength environment relates to how we deal with this power variation in our electronic devices. If you own a GPS, you know this when when trying to acquire a GPS signal from a cold-start. The amount of time it takes to acquire GPS satellites can range from seconds to minutes, and sometimes we don't get a signal at all, especially if we have tree cover with branches swaying in the wind.

Explaining the variable delay in GPS comes out quite cleanly as a fat-tail statistic if you understand how the GPS locks into the set of satellite signals. The solution assumes the entropy variations of the signal strength and integrating this against the search space that the receiver needs to lock-in to the GPS satellites.

Since the search space involves time on one axis and frequency in the other, it takes in the limit ~N² steps to decode a solution that identifies a particular satellite signal sequence for your particular unknown starting position [1]. This gets reduced because of the mean number of steps needed on average in the search space. We can use some dynamic programming matrix methods and parallel processing (perhaps using an FFT) to get this to order N, so the speed-up for a given rate is t². So this will take a stochastic amount of time according to MaxEnt of :

P (t | R) = exp(-c*R*t²)

However because of the Rayleigh fading problem we don't know how long it will take to integrate our signal with regard to the rate R. This rate has a density function proportional to the power level distribution :

p (R) = k * exp(-k*R)

then according to Bayes the conditionals line up to give the probability of acquiring a signal within time t:

P (t) = integral of P(t |R) * p(R) over all R

this leads to the entropic dispersion result of:

P (t < T) = 1/(1+(T/a)²)

where a is an empirically determined number derived from k and c. I wouldn't consider this an extremely fat tail because the acceleration of the search by quadrature tends to mitigate very long times.

I grabbed some data from a GPS project that has a goal to speed up wild-fire response times by cleverly using remote transponders : The FireBug project. They published a good chunk of data for cold-start times as shown in the histogram below. Note that the data shows many times that approach 1000 seconds. The single parameter entropic dispersion fit (a=62 seconds) appears as the blue curve, and it fits the data quite well:



Interesting how we can sharpen the tail in a naturally entropic environment by applying an accelerating technology (also see oil discovery). Put this in the context of a diametrically opposite situation where the diffusion limitations of CO2 slow down the impulse response times in the atmosphere, creating huge fat-tails which will inevitably lead to global warming.

If we can think of some way to accelerate the CO2 removal, we can shorten the response time, just like we can speed up GPS acquisition times or speed up oil extraction. Or should we have just slowed down oil extraction to begin with?

How's that for some globally relevant context?

---

Notes:

[1] If you already know your position and have that stored in your GPS, the search time shrinks enormously. This is the warm or hot-start mode that is currently used by most manufacturers. The cold-start still happens if you transport a "cold" GPS to a completely different location and have to re-ascquire the position based on unknown starting coordinates.