EROEI Math

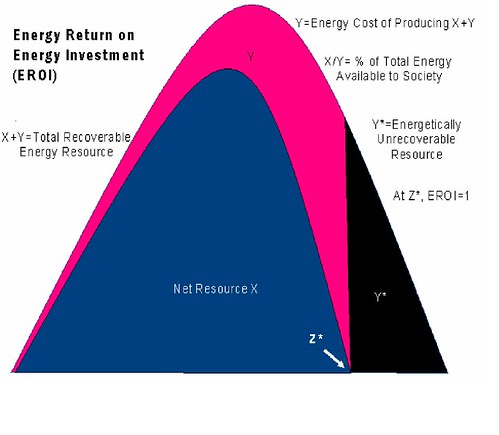
I have noticed a bit of confusion on what Energy Return on Energy Invested (EROEI) means when a fossil fuel extraction process reinvests the recovered energy and how that will serve to aggressively deplete the supply as EROEI approaches 1. Consider the case when the energy needed for extraction arises from a portion of the energy produced:

if E=EROEI
and
if P=Fraction of Energy put to use elsewhere

then
P = (E-1)/E

Notice that when E=2, we waste exactly half the energy in the regeneration process. When E=1, we waste all the energy.

Anything greater than 1 means that the process can sustain itself. The problem occurs with the huge "burn" rate we get as EROEI approaches one.

This has implications for global warming and the tremendous pressure on non-renewable resources, which acts to hasten depletion much more than an energy source with a high EROEI would.

---

Alternatively, we can look at this with a more fundamental mathematical approach and cast the energy reinvestment as a geometric series (as you would by hand). This actually converges quite nicely if you can get the math right.

Energy Reinvested = SUM ( Ei ) for i=0..N-1
Energy Produced = EN

ER/EP = SUM ((1/E)i) for i=1..N

The summation term, SUM, converges to the value (1/E)/(1-1/E) for large N (example here).

therefore,
ER/EP = 1/(E-1)

and the fraction "produced" over total energy reduces to:

P = EP/(EP+ER)=1/(1+ER/EP)=(E-1)/E

Update:

    ... a bit more formal and precise

The PeakOil message board contains a recent discussion of this effect and what it means for oil depletion. Somebody came up with the term net oil to refer to the loss due to reinvestment. One thing for certain -- it will only get worse in the future as we use petroleum with lower and lower values of EROEI.