Lotka-Volterra equation

A poster at peakoil.com, jimk, tried his hand at modifying the Logistic equation model describing oil depletion dynamics. He made a decent attempt at correcting what I always claimed as a weak spot of the Logistic model: that the Logistic formulation needs a "biological" entity to propagate exponential growth but that nothing in its derivation hints at this fundamental requirement. So, jimk made an interesting substitution as shown below:

As it turns out, his modified equation pretty much matches the Lotka-Volterra equation which biologists use to model quasi-cyclic oscillations of "renewable" resources such as foxes and rabbits as well as other "predator-prey" relationships.


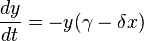
So, in jimk's equations R = population of prey and P = population of predators. R starts at some value and decays nonlinearly and proportionally to how much prey remains and how many predators exist to eat them. Similarly, the predator P starts at some value and grows proportionally to how many predators exist and how much prey exist (i.e. exponential birth rate sped up by food supply). The predator population also dies in proportion to its current population (i.e. classical death rate).

P : P*R
This only differs from the conventional L-V in that the prey does not have its own birth rate. So it generates a "non-renewable" variant of the L-V solution.

Humans = P = the predators
Oil = R = the prey

Interesting analogy, but as commenter Doly said at the peakoil.com thread:

I can see a certain logic in the way the equations are tweaked to show the economic incentives to extract oil, but it's still an oversimplified picture of the economy. And of course, there's nothing there to indicate geological constraints, which really should be there.

I agree, that the lack of geological constraints makes the rise and fall of the modified L-V equations depend solely on the non-linear interaction between the rates of change of the two populations. In effect, just as in the logistic model, the parameters have no physical meaning with respect to oil depletion. Plus, we can only solve this set of equations numerically -- which makes it hard to come up with a URR. The fact that the Logistic equation happens to generate an analytical URR and that the modified L-V doesn't means that the Logistic just got lucky. Convenience and expediency for the Logistic win out over a slightly more principled construction in the case of the L-V formulation.

But if we want a real geological constraint, the discovery/shock model remains the one to beat.

Update: I probably should take back the assertion I made regarding the difficulty in estimating the URR for the L-V equations. Even though I haven't verified it through the computational wringer, I suspect that the URR corresponds to the initial value for R(0) (i.e. R(t) at time=0).